Figure: A buzzer.
Figure 1 displays a buzzer consists of a relay connected to a battery by a switch that is opened when the relay operates. If the switch is on, the relay operates and opens the switch which turns off the relay which closes the switch. Thus the circuit oscillates and never settles down to a stable state.
The buzzer formalization has only internal events--at least once it is started, and this makes its operation easy to formalize.
State constraint axioms for formalizing a buzzer analogous to those often used for the stuffy room scenario would be immediately contradictory, asserting that the relay is on if and only if it is off. Our present situation calculus formalism follows human common sense reasoning directly and requires no special causal formalism or logic with implications not equivalent to their contrapositives.
There are effect axioms and occurrence axioms. The former are well known and give the effects of events. The latter assert that in situations in which certain fluents hold, certain events will occur.
We distinguish between the fluent ![]() asserting that the
switch is on and the event
asserting that the
switch is on and the event ![]() that turns the switch on.
The fluent holding in a situation is asserted by
that turns the switch on.
The fluent holding in a situation is asserted by
![]() .
Likewise for the fluent
.
Likewise for the fluent ![]() and the event
and the event ![]() that concern the relay. We also have
that concern the relay. We also have ![]() and
and 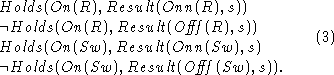 for the switch and the relay.
for the switch and the relay.
Effect axioms:
Occurrence axioms:
Note that each of the above occurrence axioms has a second term in the precondition. They are needed to avoid unwanted concurrent events.
Frame assertions--for now axioms:
These frame assertions tell what doesn't change. They are few enough in this case, since there are few actions and few fluents. In general it is more efficient to say what does change. In this case we have
In section 6 we describe how to get the frame assertions by circumscribing Changes(e,f,s).
Let an initial situation, called S0, be given by
We can proceed a step at a time. We have
in accordance with (4). Hence
and therefore, letting
we have
Some elaborations of the buzzer axioms will be worth doing.
1. Allow the action of stopping the buzzer to occur at any situation.
2. Consider the action of stopping the buzzer as a concurrent event.
3. A concurrency elaboration along the lines of [McC92] and [MC98] might be to have two non synchronized buzzers B1 and B2 with no guaranteed temporal relation between the events involving B1 and B2.