

Next: Actions and other events
Up: ACTIONS AND OTHER EVENTS
Previous: The blocks world
We use circumscription to minimize the events that occur in a
situation, the fluents that might prevent an event from having its
standard effect, and the changes in fluents. In contrast to the
formalism of [McC86] which minimized predicates over all the
arguments, we minimize for each successive situation separately.
However, in doing this minimization in s we take as fixed the
Holds(f,s) sentences and the 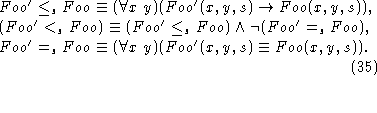 sentences
inferred from the effects of the event that led to the situation. We
are giving up the possibility of trading and abnormality in one
situation for an abnormality in another.
Doing the nonmonotonic reasoning in situations successively
corresponds to the way people predict the consequences of sequences of
actions and events. It seems to give the same conclusions as Yoav
Shoham's chronological minimization [Sho88] but is
computationally more straightforward. Like chronological minimization,
it avoids the Yale shooting problem and its friends.
sentences
inferred from the effects of the event that led to the situation. We
are giving up the possibility of trading and abnormality in one
situation for an abnormality in another.
Doing the nonmonotonic reasoning in situations successively
corresponds to the way people predict the consequences of sequences of
actions and events. It seems to give the same conclusions as Yoav
Shoham's chronological minimization [Sho88] but is
computationally more straightforward. Like chronological minimization,
it avoids the Yale shooting problem and its friends.
However, we advocate this only for projection problems, i.e. reasoning
about the future from information about the past. The method is not
appropriate for the stolen car scenario in which one has to
reason from an assertion (that the car is missing) about a later
situation.

With the present formalism, the person or agent setting up the problem
must know that projection forward in time is appropriate. It would be
better if this were a consequence of the formalized facts.
Now let's consider circumscribing at each situation separately. The
simplest case is when we have a predicate Foo(x,y,s).
We write the axioms
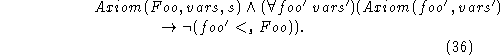
Then the circumscription of Foo(x,y,s) takes the form
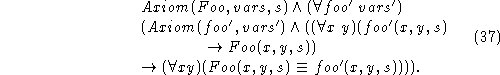
Here vars stands for a list of the entities being varied as Foo is
minimized.
This spells out to
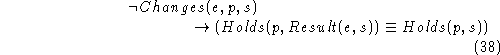
Call this formula Circ(Axiom;Foo;vars;s). This is the notation of
[Lif94] with the addition of the argument s to say
that s is kept fixed.
The general frame axioms are
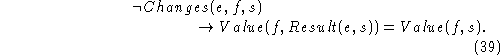
for propositional fluents and

for general fluents.
Suppose we allow complex fluents, say 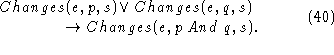 when p and q are
propositional fluents. We then need an axiom
when p and q are
propositional fluents. We then need an axiom
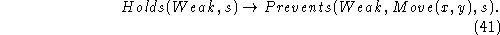
Similar axioms are required for the other propositional functions of
fluents and for the compositions of non-propositional fluents.
[This leads to difficulties when we want to delimit what changes,
since there are arbitrarily complex compositions of fluents. We'll
confine ourselves to elementary fluents for now by not putting
compositions in the language.]
In these circumscriptions we also minimize Holds.
This tolerates elaborations like

If Holds(Weak,s) isn't asserted, Move(x,y) will not be prevented.
Lin and Shoham, [LS95] consider a theory of action to be
provably correct if doing the nonmonotonic reasoning results in
a complete nonmonotonic theory of the action. This seems like a
worthy goal, but I don't know if the present theory achieves it.


Next: Actions and other events
Up: ACTIONS AND OTHER EVENTS
Previous: The blocks world
John McCarthy
Fri Feb 8 17:29:20 PST 2002
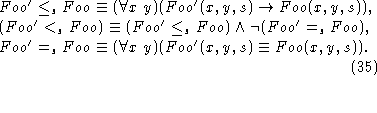 sentences
inferred from the effects of the event that led to the situation. We
are giving up the possibility of trading and abnormality in one
situation for an abnormality in another.
Doing the nonmonotonic reasoning in situations successively
corresponds to the way people predict the consequences of sequences of
actions and events. It seems to give the same conclusions as Yoav
Shoham's chronological minimization [Sho88] but is
computationally more straightforward. Like chronological minimization,
it avoids the Yale shooting problem and its friends.
sentences
inferred from the effects of the event that led to the situation. We
are giving up the possibility of trading and abnormality in one
situation for an abnormality in another.
Doing the nonmonotonic reasoning in situations successively
corresponds to the way people predict the consequences of sequences of
actions and events. It seems to give the same conclusions as Yoav
Shoham's chronological minimization [Sho88] but is
computationally more straightforward. Like chronological minimization,
it avoids the Yale shooting problem and its friends.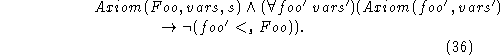
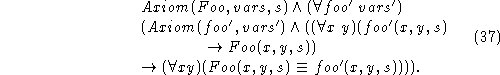
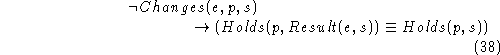
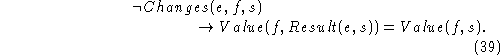
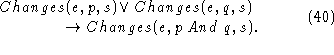 when p and q are
propositional fluents. We then need an axiom
when p and q are
propositional fluents. We then need an axiom
