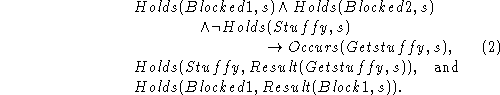
Situations are denoted by the letter s decorated with subscripts. Constants like S0 are capitalized, and variables are lower case. However, we do not assume that all situations are generated from a big bang situation S0 as does Reiter [Rei01].
The sentence Holds(pfluent,s) asserts that the propositional fluent pfluent holds in the situation s. Sometimes we write just pfluent(s), but the notation with Holds allows quantifying over fluents. We also have term fluents, and Value(tfluent,s) gives the value of tfluent in the situation s. We also sometimes write just tfluent(s).
Result(e,s) denotes the situation that arises when the event e occurs in the situation s. In this simple formalism, neither situations nor events have durations.
Occurs(e,s) is the assertion that the event e occurs in the situation s.
Next(s) is the next situation after s. It is defined by
for those situations in which an occurrence assertion determines what event will occur.
As an example, three of the axioms of the stuffy room phenomenon are
Getstuffy is an internal event and occurs all by itself when the vents are blocked.
We use circumscription to minimize occurrences, to minimize change (frame problem), and to minimize the fluents that prevent actions and other events (qualification problem).
Treating internal and external events by the same formalism admits elaborations that turn some instances of external events into internal events. Thus we can elaborate the stuffy room scenario by adjoining an occurrence axiom saying that when the room becomes stuffy, someone unblocks a vent, which makes the room unstuffy. The further elaboration that when a vent is unblocked, someone blocks it again, perhaps from feeling cold, causes the system to oscillate and never settle down.
An external event can create a situation in which the occurrence axiom for an internal event is satisfied. This leads to a new situation in which a new internal event can occur. When no more internal events occur the process settles down, and we can infer a statement about the resulting stable state. Stable states are usually characterized by state constraints. In physics these states often minimize potential energy.
The next three sections discuss examples, a buzzer which has only internal events, the stuffy room scenario, and the blocks world.