We shall first define a class of symbolic expressions in terms
of ordered pairs and lists. Then we shall define five elementary
functions and predicates, and build from them by composition,
conditional expressions, and recursive definitions an extensive class
of functions of which we shall give a number of examples. We shall
then show how these functions themselves can be expressed as symbolic
expressions, and we shall define a universal function ![]() that
allows us to compute from the expression for a given function its
value for given arguments. Finally, we shall define some functions
with functions as arguments and give some useful examples.
that
allows us to compute from the expression for a given function its
value for given arguments. Finally, we shall define some functions
with functions as arguments and give some useful examples.
a. A Class of Symbolic Expressions. We shall now define the S-expressions (S stands for symbolic). They are formed by using the special characters
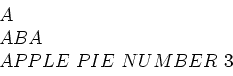
There is a twofold reason for departing from the usual
mathematical practice of using single letters for atomic
symbols. First, computer programs frequently require hundreds of
distinguishable symbols that must be formed from the 47 characters
that are printable by the IBM 704 computer. Second, it is convenient
to allow English words and phrases to stand for atomic entities for
mnemonic reasons. The symbols are atomic in the sense that any
substructure they may have as sequences of characters is ignored. We
assume only that different symbols can be distinguished.
S-expressions are then defined as follows:
1. Atomic symbols are S-expressions.
2. If ![]() and
and ![]() are S-expressions, so is
are S-expressions, so is
![]() .
.
Examples of S-expressions are
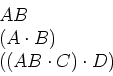
l. ![]() stands for (m
stands for (m ![]() ).
).
2.
![]() stands for
stands for
![]() .
.
3.
![]() stands for
stands for
![]() .
.
Subexpressions can be similarly abbreviated. Some examples of these abbreviations are
![]() for
for
![]() for
for
![]()
Since we regard the expressions with commas as abbreviations
for those not involving commas, we shall refer to them all as
S-expressions.
b. Functions of S-expressions and the Expressions That Represent Them. We now define a class of functions of S-expressions. The expressions representing these functions are written in a conventional functional notation. However, in order to clearly distinguish the expressions representing functions from S-expressions, we shall use sequences of lower-case letters for function names and variables ranging over the set of S-expressions. We also use brackets and semicolons, instead of parentheses and commas, for denoting the application of functions to their arguments. Thus we write
c. The Elementary S-functions and Predicates. We introduce the following functions and predicates:
1. atom. atom[x] has the value of T or F according
to whether x is an atomic symbol. Thus
atom [X] = T
atom [(X ![]() A)] = F
A)] = F
2. eq. eq [x;y] is defined if and only if both x and y are
atomic. eq [x; y] = T if x and y are the same symbol, and eq [x; y] =
F otherwise. Thus
eq [X; X] = T
eq [X; A] = F
eq [X; (X ![]() A)] is undefined.
A)] is undefined.
3. car. car[x] is defined if and only if x is not atomic.
car
![]() . Thus car [X] is undefined.
. Thus car [X] is undefined.
car ![]() = X
= X
car
![]()
4. cdr. cdr [x] is also defined when x is not atomic. We have
cdr
![]() . Thus cdr [X] is undefined.
. Thus cdr [X] is undefined.
cdr ![]() = A
cdr
= A
cdr
![]() = Y
= Y
5. cons. cons [x; y] is defined for any x and y. We have cons
![]() . Thus
. Thus
cons [X; A] = (X A)
cons
![]()
car, cdr, and cons are easily seen to satisfy the relations
car [cons [x; y]] = x
cdr [cons [x; y]] = y
cons [car [x]; cdr [x]] = x, provided that x is not atomic.
The names ``car'' and ``cons'' will come to have mnemonic
significance only when we discuss the representation of the system in
the computer. Compositions of car and cdr give the subexpressions of a
given expression in a given position. Compositions of cons form
expressions of a given structure out of parts. The class of functions
which can be formed in this way is quite limited and not very
interesting.
d. Recursive S-functions. We get a much larger class of functions (in fact, all computable functions) when we allow ourselves to form new functions of S-expressions by conditional expressions and recursive definition. We now give some examples of functions that are definable in this way.
1. ![]() . The value of
. The value of ![]() is the first atomic symbol of
the S-expression
is the first atomic symbol of
the S-expression ![]() with the parentheses ignored. Thus
with the parentheses ignored. Thus
We have
We now trace in detail the steps in the evaluation of
ff [((A ![]() B)
B) ![]() C)]:
C)]:
ff [((A ![]() B)
B) ![]() C)]
C)]
![\begin{eqnarray*}
&=& [atom [((A \cdot B) \cdot C)] \rightarrow((A \cdot B) \cdo...
...&=& [T \rightarrow A;T \rightarrow {\rm ff}[car[A]]]\ \\
&=& A
\end{eqnarray*}](img101.png)
2. subst ![]() . This function gives the result of
substituting the S-expression
. This function gives the result of
substituting the S-expression ![]() for all occurrences of the
atomic symbol
for all occurrences of the
atomic symbol ![]() in the S-expression
in the S-expression ![]() . It is defined by
. It is defined by
subst [x; y; z] = [atom [z] ![]() [eq [z; y]
[eq [z; y] ![]() x;
T
x;
T ![]() z];
z];
![]() T
T ![]() cons [subst [x; y; car [z]]; subst [x; y; cdr [z]]]]
cons [subst [x; y; car [z]]; subst [x; y; cdr [z]]]]
As an example, we have
3. equal [x; y]. This is a predicate that has the value ![]() if
if ![]() and
and ![]() are the same S-expression, and has the value F otherwise. We have
are the same S-expression, and has the value F otherwise. We have
equal [x; y] = [atom [x]atom [y]
eq [x; y]]
atom [x]
atom [y]
equal [car [x]; car [y]]
equal [cdr [x]; cdr [y]]]
It is convenient to see how the elementary functions look in
the abbreviated list notation. The reader will easily verify that
(i)
![]()
(ii)
![]()
(iii)
![]()
(iv)
![]()
(v)
![]()
We define
![]()
This predicate is useful in dealing with lists.
Compositions of car and cdr arise so frequently that many
expressions can be written more concisely if we abbreviate
![]() for
for
![]()
![]() for
for
![]() , etc.
, etc.
Another useful abbreviation is to write list
![]()
for
![]() .
.
This function gives the list,
![]() , as a function of its elements.
, as a function of its elements.
The following functions are useful when S-expressions are regarded as lists.
1. append [x;y].
append [x; y] = [null[x] ![]() y; T
y; T ![]() cons [car [x];
append [cdr [x]; y]]]
cons [car [x];
append [cdr [x]; y]]]
An example is
append [(A, B); (C, D, E)] = (A, B, C, D, E)
2. among [x;y]. This predicate is true if the S-expression ![]() occurs among the elements of the list
occurs among the elements of the list ![]() . We have
. We have
3. pair [x;y]. This function gives the list of pairs of
corresponding elements of the lists ![]() and
and ![]() . We have
. We have
4. assoc [x;y]. If ![]() is a list of the form
is a list of the form
![]() and
and ![]() is one of the
is one of the ![]() 's, then assoc
's, then assoc ![]() is the corresponding
is the corresponding ![]() . We have
. We have
An example is
5. ![]() . Here
. Here ![]() is assumed to have the form of a list of
pairs
is assumed to have the form of a list of
pairs
![]() , where the
, where the ![]() 's are atomic,
and
's are atomic,
and ![]() may be any S-expression. The value of
may be any S-expression. The value of ![]() is the result
of substituting each
is the result
of substituting each ![]() for the corresponding
for the corresponding ![]() in
in ![]() . In order to define
sublis, we first define an auxiliary function. We have
. In order to define
sublis, we first define an auxiliary function. We have
We have
sublis [((X, (A, B)), (Y, (B, C))); (A, X ![]() Y)]
= (A, (A, B), B, C)
Y)]
= (A, (A, B), B, C)
e. Representation of S-Functions by S-Expressions. S-functions have been described by M-expressions. We now give a rule for translating M-expressions into S-expressions, in order to be able to use S-functions for making certain computations with S-functions and for answering certain questions about S-functions.
The translation is determined by the following rules in rich we denote
the translation of an M-expression ![]() by
by ![]() *.
*.
1. If ![]() is an S-expression
is an S-expression ![]() * is (QUOTE,
* is (QUOTE, ![]() ).
).
2. Variables and function names that were represented by strings of lower-case letters are translated to the corresponding strings of the corresponding uppercase letters. Thus car* is CAR, and subst* is SUBST.
3. A form
![]() is translated to
is translated to
![]() Thus cons [car [x]; cdr [x]]
Thus cons [car [x]; cdr [x]]![]() is (CONS, (CAR, X), (CDR, X)).
is (CONS, (CAR, X), (CDR, X)).
4.
![]() is
(COND,
is
(COND,
![]() .
.
5.
![]() is (LAMBDA,
is (LAMBDA,
![]() .
.
6.
![]() is (LABEL, a
is (LABEL, a![]() ,
, ![]() .
.
With these conventions the substitution function whose
M-expression is label [subst; ![]() [[x; y; z]; [atom [z]
[[x; y; z]; [atom [z] ![]() [eq [y; z]
[eq [y; z] ![]() x; T
x; T ![]() z]; T
z]; T ![]() cons [subst [x; y; car [z]]; subst [x; y; cdr [z]]]]]] has the S-expression
cons [subst [x; y; car [z]]; subst [x; y; cdr [z]]]]]] has the S-expression
(LABEL, SUBST, (LAMBDA, (X, Y, Z), (COND ((ATOM, Z), (COND, (EQ, Y, Z), X), ((QUOTE, T), Z))), ((QUOTE, T), (CONS, (SUBST, X, Y, (CAR Z)), (SUBST, X, Y, (CDR, Z)))))))
This notation is writable and somewhat readable. It can be made easier to read and write at the cost of making its structure less regular. If more characters were available on the computer, it could be improved considerably.5
f. The Universal S-Function apply. There is an S-function
![]() with the property that if
with the property that if ![]() is an S-expression for an S-function
is an S-expression for an S-function
![]() and
and ![]() is a list of arguments of the form
is a list of arguments of the form
![]() , where
, where
![]() are arbitrary S-expressions, then
are arbitrary S-expressions, then
![]() and
and
![]() are defined for the same values of
are defined for the same values of
![]() , and are equal when defined. For example,
, and are equal when defined. For example,
eval[e; a] = [
atom [e] ![]() assoc [e; a];
assoc [e; a];
atom [car [e]] ![]() [
[
eq [car [e]; QUOTE] ![]() cadr [e];
cadr [e];
eq [car [e]; ATOM] ![]() atom [eval [cadr [e]; a]];
atom [eval [cadr [e]; a]];
eq [car [e]; EQ] ![]() [eval [cadr [e]; a] = eval [caddr [e]; a]];
[eval [cadr [e]; a] = eval [caddr [e]; a]];
eq [car [e]; COND] ![]() evcon [cdr [e]; a];
evcon [cdr [e]; a];
eq [car [e]; CAR] ![]() car [eval [cadr [e]; a]];
car [eval [cadr [e]; a]];
eq [car [e]; CDR] ![]() cdr [eval [cadr [e]; a]];
cdr [eval [cadr [e]; a]];
eq [car [e]; CONS] ![]() cons [eval [cadr [e]; a]; eval [caddr [e];
cons [eval [cadr [e]; a]; eval [caddr [e];
a]]; T ![]() eval [cons [assoc [car [e]; a];
eval [cons [assoc [car [e]; a];
evlis [cdr [e]; a]]; a]];
eq [caar [e]; LABEL] ![]() eval [cons [caddar [e]; cdr [e]];
eval [cons [caddar [e]; cdr [e]];
cons [list [cadar [e]; car [e]; a]];
eq [caar [e]; LAMBDA] ![]() eval [caddar [e];
eval [caddar [e];
append [pair [cadar [e]; evlis [cdr [e]; a]; a]]]
and
We now explain a number of points about these definitions. 6
1. ![]() itself forms an expression representing the value of
the function applied to the arguments, and puts the work of evaluating
this expression onto a function
itself forms an expression representing the value of
the function applied to the arguments, and puts the work of evaluating
this expression onto a function ![]() . It uses
. It uses ![]() to put quotes
around each of the arguments, so that
to put quotes
around each of the arguments, so that ![]() will regard them as
standing for themselves.
will regard them as
standing for themselves.
2. ![]() has two arguments, an expression
has two arguments, an expression ![]() to be
evaluated, and a list of pairs
to be
evaluated, and a list of pairs ![]() . The first item of each pair is an
atomic symbol, and the second is the expression for which the symbol
stands.
. The first item of each pair is an
atomic symbol, and the second is the expression for which the symbol
stands.
3. If the expression to be evaluated is atomic, eval evaluates
whatever is paired with it first on the list ![]() .
.
4. If ![]() is not atomic but
is not atomic but ![]() is atomic, then the expression
has one of the forms
is atomic, then the expression
has one of the forms ![]() or
or ![]() or
or
![]() or
or
![]() , or
, or ![]() or
or ![]() or
or
![]() or
or
![]() where
where ![]() is an
atomic symbol.
is an
atomic symbol.
In the case ![]() the expression
the expression ![]() , itself, is taken. In
the case of
, itself, is taken. In
the case of ![]() or
or ![]() or
or ![]() the expression
the expression ![]() is
evaluated and the appropriate function taken. In the case of
is
evaluated and the appropriate function taken. In the case of
![]() or
or
![]() two expressions have to be evaluated. In the
case of
two expressions have to be evaluated. In the
case of
![]() the
the ![]() 's have to be
evaluated
in order until a true
's have to be
evaluated
in order until a true ![]() is found, and then the corresponding
is found, and then the corresponding ![]() must be
evaluated. This is accomplished by
must be
evaluated. This is accomplished by ![]() . Finally, in the case of
. Finally, in the case of
![]() we evaluate the expression that results from
replacing
we evaluate the expression that results from
replacing ![]() in this expression by whatever it is paired with in the
list
in this expression by whatever it is paired with in the
list ![]() .
.
5. The evaluation of
![]() is
accomplished by evaluating
is
accomplished by evaluating
![]() with the
pairing
with the
pairing
![]() put on the front
of the previous list
put on the front
of the previous list ![]() of pairs.
of pairs.
6. Finally, the evaluation of
![]() is accomplished by evaluating
is accomplished by evaluating ![]() with the list of
pairs
with the list of
pairs
![]() put on the front of the
previous list
put on the front of the
previous list ![]() .
.
The list ![]() could be eliminated, and LAMBDA and LABEL
expressions evaluated by substituting the arguments for the variables
in the expressions
could be eliminated, and LAMBDA and LABEL
expressions evaluated by substituting the arguments for the variables
in the expressions ![]() . Unfortunately, difficulties involving collisions
of bound variables arise, but they are avoided by using the list
. Unfortunately, difficulties involving collisions
of bound variables arise, but they are avoided by using the list ![]() .
.
Calculating the values of functions by using ![]() is an
activity better suited to electronic computers than to people. As an
illustration, however, we now give some of the steps for calculating
is an
activity better suited to electronic computers than to people. As an
illustration, however, we now give some of the steps for calculating
apply [(LABEL, FF, (LAMBDA, (X), (COND, (ATOM, X), X), ((QUOTE, T),(FF, (CAR, X))))));((A![]() B))] = A
B))] = A
The first argument is the S-expression that represents the function ff
defined in section 3d. We shall abbreviate it by using the letter
![]() . We have
. We have
[; ( (A
B) )]
= eval [((LABEL, FF,
), (QUOTE, (A
B))); NIL]
whereis the part of
beginning (LAMBDA
= eval[((LAMBDA, (X),), (QUOTE, (A
B)));((FF,
))]
whereis the part of
beginning (COND
= eval [(COND, ()); ((X, (QUOTE, (A
B) ) ), (FF,
) )]
Denoting ((X, (QUOTE, (AB))), (FF,
)) by
, we obtain
= evcon [((), (
));
]
This involves eval []
= eval [( ATOM, X);]
= atom [eval [X;]]
= atom [eval [assoc [X; ((X, (QUOTE, (AB))), (FF,
))];
]]
= atom [eval [(QUOTE, (AB));
]]
= atom [(A
B)],
= F
Our main calulation continues with
[; ((A
B))]
= evcon [((
],
involves eval [] = eval [(QUOTE, T);
] = T
Our main calculation again continues with
[; ((A
B))]
= eval [
]
= eval [(FF, (CAR, X));
]
= eval [Cons [
; evlis [((CAR, X));
]];
]
Evaluating evlis [((CAR, X));
] involves
[(CAR, X);]
= car [eval [X;
]]
= car [(A
B)], where we took steps from the earlier computation of atom [eval [X;
]] = A,
so evlis [((CAR, X));] then becomes
list [list [QUOTE; A]] = ((QUOTE, A)),
our main quantity becomes
= eval [(
, (QUOTE, A));
]
The subsequent steps are made as in the beginning of the
calculation. The LABEL and LAMBDA cause new pairs to be added to ![]() ,
which gives a new list of pairs
,
which gives a new list of pairs ![]() . The
. The ![]() term of the conditional
eval [(ATOM, X);
term of the conditional
eval [(ATOM, X); ![]() ] has the value T because X is paired with (QUOTE,
A) first in
] has the value T because X is paired with (QUOTE,
A) first in ![]() , rather than with (QUOTE, (A
, rather than with (QUOTE, (A![]() B)) as in
B)) as in ![]() .
.
Therefore we end up with eval [X; ![]() ] from the
] from the ![]() , and
this is just A.
, and
this is just A.
g. Functions with Functions as Arguments. There are a number of
useful functions some of whose arguments are functions. They are
especially useful in defining other functions. One such function is
![]() with an S-expression argument
with an S-expression argument ![]() and an argument
and an argument ![]() that
is a function from S-expressions to S-expressions. We define
that
is a function from S-expressions to S-expressions. We define
1. An atomic symbol is an allowed expression.
2. If
![]() are allowed expressions, ( PLUS,
are allowed expressions, ( PLUS,
![]() ) and (TIMES,
) and (TIMES,
![]() ) are also, and represent the sum and product, respectively, of
) are also, and represent the sum and product, respectively, of
![]() .
.
This is, essentially, the Polish notation for functions, except that the inclusion of parentheses and commas allows functions of variable numbers of arguments. An example of an allowed expression is (TIMES, X, (PLUS, X, A), Y), the conventional algebraic notation for which is X(X + A)Y.
Our differentiation formula, which gives the derivative of ![]() with respect to
with respect to ![]() , is
, is
diff [y; x] = [atom [y] ![]() [eq [y; x]
[eq [y; x] ![]() ONE; T
ONE; T ![]() ZERO]; eq [car [Y]; PLUS]
ZERO]; eq [car [Y]; PLUS] ![]() cons [PLUS; maplist [cdr [y];
cons [PLUS; maplist [cdr [y]; ![]() [[z]; diff [car [z]; x]]]]; eq[car [y]; TIMES]
[[z]; diff [car [z]; x]]]]; eq[car [y]; TIMES] ![]() cons[PLUS;
maplist[cdr[y];
cons[PLUS;
maplist[cdr[y]; ![]() [[z]; cons [TIMES; maplist[cdr [y];
[[z]; cons [TIMES; maplist[cdr [y]; ![]() [[w];
[[w]; ![]() eq [z; w]
eq [z; w] ![]() car [w]; T
car [w]; T ![]() diff [car [[w]; x]]]]]]]
diff [car [[w]; x]]]]]]]
The derivative of the expression (TIMES, X, (PLUS, X, A), Y), as computed by this formula, is
(PLUS, (TIMES, ONE, (PLUS, X, A), Y), (TIMES, X, (PLUS, ONE, ZERO), Y), (TIMES, X, (PLUS, X, A), ZERO))
Besides ![]() , another useful function with functional arguments
is
, another useful function with functional arguments
is ![]() , which is defined as
, which is defined as