The LISP Programming System

The LISP programming system is a system for using the IBM 704 computer to compute with symbolic information in the form of S-expressions. It has been or will be used for the following purposes:

l. Writing a compiler to compile LISP programs into machine language.

2. Writing a program to check proofs in a class of formal logical systems.

3. Writing programs for formal differentiation and integration.

4. Writing programs to realize various algorithms for generating proofs in predicate calculus.

5. Making certain engineering calculations whose results are formulas rather than numbers.

6. Programming the Advice Taker system.

The basis of the system is a way of writing computer programs to evaluate S-functions. This will be described in the following sections.

In addition to the facilities for describing S-functions, there are facilities for using S-functions in programs written as sequences of statements along the lines of FORTRAN (4) or ALGOL (5). These features will not be described in this article.

a. Representation of S-Expressions by List Structure. A list structure is a collection of computer words arranged as in figure 1a or 1b. Each word of the list structure is represented by one of the subdivided rectangles in the figure. The $left$ box of a rectangle represents the $address$ field of the word and the $right$ box represents the $decrement$ field. An arrow from a box to another rectangle means that the field corresponding to the box contains the location of the word corresponding to the other rectangle.

Fig. 1

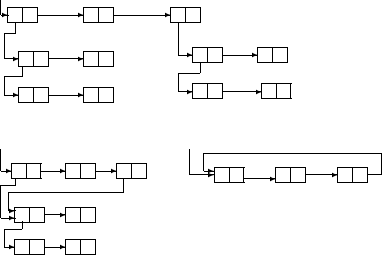
It is permitted for a substructure to occur in more than one place in a list structure, as in figure 1b, but it is not permitted for a structure to have cycles, as in figure 1c. An atomic symbol is represented in the computer by a list structure of special form called the association list of the symbol. The address field of the first word contains a special constant which enables the program to tell that this word represents an atomic symbol. We shall describe association lists in section 4b.

An S-expression $x$ that is not atomic is represented by a word, the address and decrement parts of which contain the locations of the subexpressions $car[x]$ and $cdr[x]$, respectively. If we use the symbols $A$, $B,$ etc. to denote the locations of the association list of these symbols, then the S-expression $((A\cdot B)\cdot (C\cdot (E\cdot F)))$ is represented by the list structure $a$ of figure 2. Turning to the list form of S-expressions, we see that the S-expression $(A, (B, C), D)$, which is an abbreviation for $(A\cdot ((B\cdot (C\cdot NIL))\cdot (D\cdot NIL)))$, is represented by the list structure of figure 2b.

Figure 2

When a list structure is regarded as representing a list, we see that each term of the list occupies the address part of a word, the decrement part of which $points$ to the word containing the next term, while the last word has NIL in its decrement.

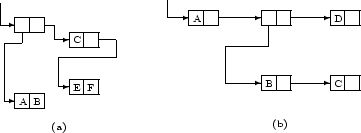
An expression that has a given subexpression occurring more than once can be represented in more than one way. Whether the list structure for the subexpression is or is not repeated depends upon the history of the program. Whether or not a subexpression is repeated will make no difference in the results of a program as they appear outside the machine, although it will affect the time and storage requirements. For example, the S-expression ((A$\cdot$B)$\cdot$(A$\cdot$B)) can be represented by either the list structure of figure 3a or 3b.

Figure 3

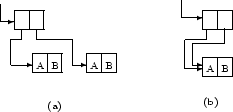
The prohibition against circular list structures is essentially a prohibition against an expression being a subexpression of itself. Such an expression could not exist on paper in a world with our topology. Circular list structures would have some advantages in the machine, for example, for representing recursive functions, but difficulties in printing them, and in certain other operations, make it seem advisable not to use them for the present.

The advantages of list structures for the storage of symbolic expressions are:

1. The size and even the number of expressions with which the program will have to deal cannot be predicted in advance. Therefore, it is difficult to arrange blocks of storage of fixed length to contain them.

2. Registers can be put back on the free-storage list when they are no longer needed. Even one register returned to the list is of value, but if expressions are stored linearly, it is difficult to make use of blocks of registers of odd sizes that may become available.

3. An expression that occurs as a subexpression of several expressions need be represented in storage only once.

b. Association Lists⁷. In the LISP programming system we put more in the association list of a symbol than is required by the mathematical system described in the previous sections. In fact, any information that we desire to associate with the symbol may be put on the association list. This information may include: the print name, that is, the string of letters and digits which represents the symbol outside the machine; a numerical value if the symbol represents a number; another S-expression if the symbol, in some way, serves as a name for it; or the location of a routine if the symbol represents a function for which there is a machine-language subroutine. All this implies that in the machine system there are more primitive entities than have been described in the sections on the mathematical system.

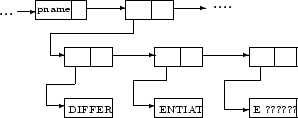
For the present, we shall only describe how print names are represented on association lists so that in reading or printing the program can establish a correspondence between information on punched cards, magnetic tape or printed page and the list structure inside the machine. The association list of the symbol DIFFERENTIATE has a segment of the form shown in figure 4. Here $pname$ is a symbol that indicates that the structure for the print name of the symbol whose association list this is hanging from the next word on the association list. In the second row of the figure we have a list of three words. The address part of each of these words points to a Word containing six 6-bit characters. The last word is filled out with a 6-bit combination that does not represent a character printable by the computer. (Recall that the IBM 7O4 has a 36-bit word and that printable characters are each represented by 6 bits.) The presence of the words with character information means that the association lists do not themselves represent S-expressions, and that only some of the functions for dealing with S-expressions make sense within an association list.

Figure 4

c. Free-Storage List. At any given time only a part of the memory reserved for list structures will actually be in use for storing S-expressions. The remaining registers (in our system the number, initially, is approximately 15,000) are arranged in a single list called the free-storage list. A certain register, FREE, in the program contains the location of the first register in this list. When a word is required to form some additional list structure, the first word on the free-storage list is taken and the number in register FREE is changed to become the location of the second word on the free-storage list. No provision need be made for the user to program the return of registers to the free-storage list.

This return takes place automatically, approximately as follows (it is necessary to give a simplified description of this process in this report): There is a fixed set of base registers in the program which contains the locations of list structures that are accessible to the program. Of course, because list structures branch, an arbitrary number of registers may be involved. Each register that is accessible to the program is accessible because it can be reached from one or more of the base registers by a chain of $car$ and $cdr$ operations. When the contents of a base register are changed, it may happen that the register to which the base register formerly pointed cannot be reached by a $car-cdr$ chain from any base register. Such a register may be considered abandoned by the program because its contents can no longer be found by any possible program; hence its contents are no longer of interest, and so we would like to have it back on the free-storage list. This comes about in the following way.

Nothing happens until the program runs out of free storage. When a free register is wanted, and there is none left on the free-storage list, a reclamation⁸ cycle starts.

First, the program finds all registers accessible from the base registers and makes their signs negative. This is accomplished by starting from each of the base registers and changing the sign of every register that can be reached from it by a $car-cdr$ chain. If the program encounters a register in this process which already has a negative sign, it assumes that this register has already been reached.

After all of the accessible registers have had their signs changed, the program goes through the area of memory reserved for the storage of list structures and puts all the registers whose signs were not changed in the previous step back on the free-storage list, and makes the signs of the accessible registers positive again.

This process, because it is entirely automatic, is more convenient for the programmer than a system in which he has to keep track of and erase unwanted lists. Its efficiency depends upon not coming close to exhausting the available memory with accessible lists. This is because the reclamation process requires several seconds to execute, and therefore must result in the addition of at least several thousand registers to the free-storage list if the program is not to spend most of its time in reclamation.

d. Elementary S-Functions in the Computer. We shall now describe the computer representations of $atom$, = , $car$, $cdr$, and $cons$. An S-expression is communicated to the program that represents a function as the location of the word representing it, and the programs give S-expression answers in the same form.

$atom$. As stated above, a word representing an atomic symbol has a special constant in its address part: $atom$ is programmed as an open subroutine that tests this part. Unless the M-expression $atom[e]$ occurs as a condition in a conditional expression, the symbol $T$ or $F$ is generated as the result of the test. In case of a conditional expression, a conditional transfer is used and the symbol $T$ or $F$ is not generated.

$eq$. The program for $eq[e;f]$ involves testing for the numerical equality of the locations of the words. This works because each atomic symbol has only one association list. As with $atom$, the result is either a conditional transfer or one of the symbols $T$ or $F$.

$car$. Computing $car[x]$ involves getting the contents of the address part of register $x$. This is essentially accomplished by the single instruction CLA 0, i, where the argument is in index register, and the result appears in the address part of the accumulator. (We take the view that the places from which a function takes its arguments and into which it puts its results are prescribed in the definition of the function, and it is the responsibility of the programmer or the compiler to insert the required datamoving instructions to get the results of one calculation in position for the next.) (``car'' is a mnemonic for ``contents of the address part of register.'')

$cdr$. $cdr$ is handled in the same way as $car$, except that the result appears in the decrement part of the accumulator (``cdr'' stands for ``contents of the decrement part of register.'')

$cons$. The value of $cons[x;y]$ must be the location of a register that has $x$ and $y$ in its address and decrement parts, respectively. There may not be such a register in the computer and, even if there were, it would be time-consuming to find it. Actually, what we do is to take the first available register from the free-storage list, put $x$ and $y$ in the address and decrement parts, respectively, and make the value of the function the location of the register taken. (``cons'' is an abbreviation for ``construct.'')

It is the subroutine for $cons$ that initiates the reclamation when the free-storage list is exhausted. In the version of the system that is used at present $cons$ is represented by a closed subroutine. In the compiled version, $cons$ is open.

e. Representation of S-Functions by Programs. The compilation of functions that are compositions of $car$, $cdr$, and $cons$, either by hand or by a compiler program, is straightforward. Conditional expressions give no trouble except that they must be so compiled that only the $p$'s and $e$'s that are required are computed. However, problems arise in the compilation of recursive functions.

In general (we shall discuss an exception), the routine for a recursive function uses itself as a subroutine. For example, the program for $subst[x;y;z]$ uses itself as a subroutine to evaluate the result of substituting into the subexpressions $car[z]$ and $cdr[z]$. While $subst[x;y;cdr[z]]$ is being evaluated, the result of the previous evaluation of $subst[x;y;car[z]]$ must be saved in a temporary storage register. However, $subst$ may need the same register for evaluating $subst[x;y;cdr[z]]$. This possible conflict is resolved by the SAVE and UNSAVE routines that use the public push-down list ⁹. The SAVE routine is entered at the beginning of the routine for the recursive function with a request to save a given set of consecutive registers. A block of registers called the public push-down list is reserved for this purpose. The SAVE routine has an index that tells it how many registers in the push-down list are already in use. It moves the contents of the registers which are to be saved to the first unused registers in the push-down list, advances the index of the list, and returns to the program from which control came. This program may then freely use these registers for temporary storage. Before the routine exits it uses UNSAVE, which restores the contents of the temporary registers from the push-down list and moves back the index of this list. The result of these conventions is described, in programming terminology, by saying that the recursive subroutine is transparent to the temporary storage registers.

f. Status of the LISP Programming System (February 1960). A variant of the function apply described in section 5f has been translated into a program APPLY for the IBM 704. Since this routine can compute values of S-functions given their descriptions as S-expressions and their arguments, it serves as an interpreter for the LISP programming language which describes computation processes in this way.

The program APPLY has been imbedded in the LISP programming system which has the following features:

1. The programmer may define any number of S-functions by S-expressions. these functions may refer to each other or to certain S-functions represented by machine language program.

2. The values of defined functions may be computed.

3. S-expressions may be read and printed (directly or via magnetic tape).

4. Some error diagnostic and selective tracing facilities are included.

5. The programmer may have selected S-functions compiled into machine language programs put into the core memory. Values of compiled functions are computed about 60 times as fast as they would if interpreted. Compilation is fast enough so that it is not necessary to punch compiled program for future use.

6. A ``program feature'' allows programs containing assignment and go to statements in the style of ALGOL.

7. Computation with floating point numbers is possible in the system, but this is inefficient.

8. A programmer's manual is being prepared. The LISP programming system is appropriate for computations where the data can conveniently be represented as symbolic expressions allowing expressions of the same kind as subexpressions. A version of the system for the IBM 709 is being prepared.