We shall need a number of mathematical ideas and notations concerning
functions in general. Most of the ideas are well known, but the notion
of conditional expression is believed to be new2, and the use of conditional expressions permits functions to
be defined recursively in a new and convenient way.
a. Partial Functions. A partial function is a function
that is defined only on part of its domain. Partial functions
necessarily arise when functions are defined by computations
because for some values of the arguments the computation
defining the value of the function may not terminate.
However, some of our elementary functions will be
defined as partial functions.
b. Propositional Expressions and Predicates. A
propositional expression is an expression whose possible values are ![]() (for truth) and
(for truth) and ![]() (for falsity). We shall assume that the reader is
familiar with the propositional connectives
(for falsity). We shall assume that the reader is
familiar with the propositional connectives ![]() (``and''),
(``and''), ![]() (``or''), and
(``or''), and ![]() (``not''). Typical propositional expressions
are:
(``not''). Typical propositional expressions
are:
A predicate is a function whose range consists of the truth values T and F.
c. Conditional Expressions. The dependence of truth values
on the values of quantities of other kinds is expressed in mathematics
by predicates, and the dependence of truth values on other truth
values by logical connectives. However, the notations for expressing
symbolically the dependence of quantities of other kinds on truth values
is inadequate, so that English words and phrases are generally used for
expressing these dependences in texts that describe other dependences
symbolically. For example, the function ![]() x
x![]() is usually defined in words.
Conditional expressions are a device for expressing the dependence of
quantities on propositional quantities. A conditional expression has
the form
is usually defined in words.
Conditional expressions are a device for expressing the dependence of
quantities on propositional quantities. A conditional expression has
the form
where the ![]() 's are propositional expressions and the
's are propositional expressions and the ![]() 's are
expressions of any kind. It may be read, ``If
's are
expressions of any kind. It may be read, ``If ![]() then
then ![]() otherwise if
otherwise if ![]() then
then ![]() ,
, ![]() , otherwise if
, otherwise if ![]() then
then
![]() ,'' or ``
,'' or ``![]() yields
yields
![]() yields
yields ![]() .''
3
.''
3
We now give the rules for determining whether the value of
Some of the simplest applications of conditional expressions are in giving such definitions as
d. Recursive Function Definitions. By using conditional expressions we can, without circularity, define functions by formulas in which the defined function occurs. For example, we write
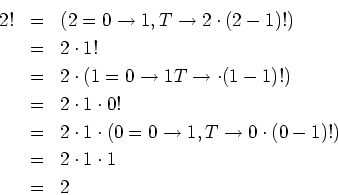
We now give two other applications of recursive function definitions. The greatest common divisor, gcd(m,n), of two positive integers m and n is computed by means of the Euclidean algorithm. This algorithm is expressed by the recursive function definition:
The Newtonian algorithm for obtaining an approximate square
root of a number ![]() , starting with an initial approximation
, starting with an initial approximation ![]() and
requiring that an acceptable approximation
and
requiring that an acceptable approximation ![]() satisfy
satisfy
![]() may be written as
may be written as
sqrt(a, x,)
= (x,T
sqrt (a,
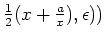
The simultaneous recursive definition of several functions is also possible, and we shall use such definitions if they are required.
There is no guarantee that the computation determined by a
recursive definition will ever terminate and, for example, an attempt
to compute n! from our definition will only succeed if ![]() is a
non-negative integer. If the computation does not terminate, the
function must be regarded as undefined for the given arguments.
is a
non-negative integer. If the computation does not terminate, the
function must be regarded as undefined for the given arguments.
The propositional connectives themselves can be defined by conditional expressions. We write
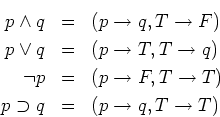
It is readily seen that the right-hand sides of the equations
have the correct truth tables. If we consider situations in which ![]() or
or
![]() may be undefined, the connectives
may be undefined, the connectives ![]() and
and ![]() are seen to be
noncommutative. For example if
are seen to be
noncommutative. For example if ![]() is false and
is false and ![]() is undefined, we see
that according to the definitions given above
is undefined, we see
that according to the definitions given above ![]() is false,
but
is false,
but ![]() is undefined. For our applications this
noncommutativity is desirable, since
is undefined. For our applications this
noncommutativity is desirable, since ![]() is computed by first
computing
is computed by first
computing ![]() , and if
, and if ![]() is false
is false ![]() is not computed. If the computation
for
is not computed. If the computation
for ![]() does not terminate, we never get around to computing
does not terminate, we never get around to computing ![]() . We shall
use propositional connectives in this sense hereafter.
. We shall
use propositional connectives in this sense hereafter.
e. Functions and Forms. It is usual in
mathematics--outside of mathematical logic--to use the word
``function'' imprecisely and to apply it to forms such as ![]() . Because we shall later compute with expressions for functions, we
need a distinction between functions and forms and a notation for
expressing this distinction. This distinction and a notation for
describing it, from which we deviate trivially, is given by Church
[3].
. Because we shall later compute with expressions for functions, we
need a distinction between functions and forms and a notation for
expressing this distinction. This distinction and a notation for
describing it, from which we deviate trivially, is given by Church
[3].
Let ![]() be an expression that stands for a function of two
integer variables. It should make sense to write
be an expression that stands for a function of two
integer variables. It should make sense to write ![]() and the
value of this expression should be determined. The expression
and the
value of this expression should be determined. The expression ![]() does not meet this requirement;
does not meet this requirement; ![]() is not a
conventional notation, and if we attempted to define it we would be
uncertain whether its value would turn out to be 13 or 19. Church
calls an expression like
is not a
conventional notation, and if we attempted to define it we would be
uncertain whether its value would turn out to be 13 or 19. Church
calls an expression like ![]() , a form. A form can be converted
into a function if we can determine the correspondence between the
variables occurring in the form and the ordered list of arguments of
the desired function. This is accomplished by Church's
, a form. A form can be converted
into a function if we can determine the correspondence between the
variables occurring in the form and the ordered list of arguments of
the desired function. This is accomplished by Church's
![]() -notation.
-notation.
If ![]() is a form in variables
is a form in variables
![]() then
then
![]() will be taken to be the function of
will be taken to be the function of
![]() variables whose value is determined by substituting the arguments
for the variables
variables whose value is determined by substituting the arguments
for the variables
![]() in that order in
in that order in ![]() and evaluating
the resulting expression. For example,
and evaluating
the resulting expression. For example,
![]() is a
function of two variables, and
is a
function of two variables, and
![]() .
.
The variables occurring in the list of variables of a
![]() -expression are dummy or bound, like variables of integration
in a definite integral. That is, we may change the names of the bound
variables in a function expression without changing the value of the
expression, provided that we make the same change for each occurrence
of the variable and do not make two variables the same that previously
were different. Thus
-expression are dummy or bound, like variables of integration
in a definite integral. That is, we may change the names of the bound
variables in a function expression without changing the value of the
expression, provided that we make the same change for each occurrence
of the variable and do not make two variables the same that previously
were different. Thus
![]() and
and
![]() denote the same function.
denote the same function.
We shall frequently use expressions in which some of the
variables are bound by ![]() 's and others are not. Such an
expression may be regarded as defining a function with parameters. The
unbound variables are called free variables.
's and others are not. Such an
expression may be regarded as defining a function with parameters. The
unbound variables are called free variables.
An adequate notation that distinguishes functions from forms allows an unambiguous treatment of functions of functions. It would involve too much of a digression to give examples here, but we shall use functions with functions as arguments later in this report.
Difficulties arise in combining functions described by
![]() -expressions, or by any other notation involving variables,
because different bound variables may be represented by the same
symbol. This is called collision of bound variables. There is a
notation involving operators that are called combinators for combining
functions without the use of variables. Unfortunately, the combinatory
expressions for interesting combinations of functions tend to be
lengthy and unreadable.
-expressions, or by any other notation involving variables,
because different bound variables may be represented by the same
symbol. This is called collision of bound variables. There is a
notation involving operators that are called combinators for combining
functions without the use of variables. Unfortunately, the combinatory
expressions for interesting combinations of functions tend to be
lengthy and unreadable.
f. Expressions for Recursive Functions. The
![]() -notation is inadequate for naming functions defined
recursively. For example, using
-notation is inadequate for naming functions defined
recursively. For example, using ![]() 's, we can convert the
definition
's, we can convert the
definition
into
In order to be able to write expressions for recursive
functions, we introduce another notation.
![]() denotes the
expression
denotes the
expression ![]() , provided that occurrences of
, provided that occurrences of ![]() within
within ![]() are to be
interpreted as referring to the expression as a whole. Thus we can
write
are to be
interpreted as referring to the expression as a whole. Thus we can
write
label(sqrt,
![]()
as a name for our sqrt function.
The symbol ![]() in label (
in label (![]() ) is also bound, that is, it may be
altered systematically without changing the meaning of the
expression. It behaves differently from a variable bound by a
) is also bound, that is, it may be
altered systematically without changing the meaning of the
expression. It behaves differently from a variable bound by a ![]() ,
however.
,
however.