In the situation calculus it is usual to specify the effects of
actions by writing effect axioms, like![]() ,
,
![]()
If we move to a formalism that allows other events to occur between s
and ![]() , then this way of specifying change needs to be
adjusted. It is possible that something might occur in the time
between s and
, then this way of specifying change needs to be
adjusted. It is possible that something might occur in the time
between s and ![]() that causes the event to have a
different result. For this reason it seems natural to allow the
preconditions, those things that hold on the left hand side, to
mention properties of all times between s and
that causes the event to have a
different result. For this reason it seems natural to allow the
preconditions, those things that hold on the left hand side, to
mention properties of all times between s and ![]() .
.
In previous versions of the situation calculus the preconditions for
an event were always modeled as a set of fluents, namely those fluents
that had to hold at s, for the event to have an effect at
![]() . If we allow other things to happen during an event,
we cannot just specify the preconditions that must hold at the
beginning of the event.
. If we allow other things to happen during an event,
we cannot just specify the preconditions that must hold at the
beginning of the event.
Consider a plane journey from Glasgow to London. It is necessary that the plane be in working order for the entire flight. It is also necessary to be in Glasgow at the beginning of the flight, but clearly, there is no need for this precondition to persist for the entire flight. It is necessary to have a ticket, until the airline steward takes it from you. This is an example of a precondition, ``having a ticket'' that must hold neither just at the moment the event starts, nor for the entire duration.
Consider another example from the Yale Shooting Problem. In order to successfully shoot a person, the gun must be loaded when the trigger is pulled, but the target must remain in the cross-hairs until the bullet hits. We represent the fact the target is in the cross-hairs by aimed. Thus we write:
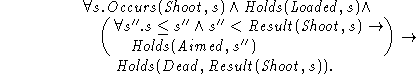
A possible objection to this example is that if the target arrives in the cross-hairs at any time before impact and remains in the path of the bullet, then they will be killed. In this case we write,
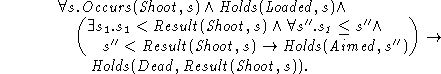
However, both these examples show the need for preconditions to be richer than a statement of what properties hold just when the event occurs. What possible properties can occur as preconditions is important because we wish to know what kinds of axioms can occur as effect axioms.
Before we consider how to represent preconditions, we recall how we
represented all possible preconditions earlier. If we wish to
introduce a predicate that can parameterize all effect axioms in the
old-fashioned situation calculus can write![]() ,
,
![]()
following [Cos97]. g is a predicate on fluents that encodes the preconditions. Parameterizing all effect axioms allows us to minimize effect axioms easily.
However, as we want to have preconditions that can extend over the duration of the event, we need more than one set of fluents. For this reason we allow as preconditions, two sets of fluents. The first set need only hold at the start of an event, while the others must persist for the entire event.
It might seem that this does not model preconditions that need hold
for only part of the duration of the event. However, we can model
these by using other defined fluents. Thus we can write that ``It is
necessary to have a ticket, until the airline steward takes it from
you.'' using a new fluent ![]() defined by
defined by
![]()
This fluent should hold for the entire![]() duration of the flight.
duration of the flight. ![]() is a shorthand for
is a shorthand for
![]() .
.
We can write ``It is necessary that the plane be in working order for the entire flight'' using the fluent WorkingOrder,
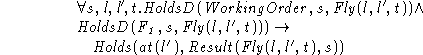
We can add `` It is necessary to
be in Glasgow![]() at the beginning of the flight''
at the beginning of the flight''

Now that our preconditions are represented as two sets![]() , rather than one,
we redefine Changes as follows:
, rather than one,
we redefine Changes as follows:
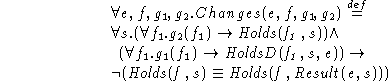
We find it useful to introduce a predicate Succeeds(e,f,s) defined as,
Frame Axioms
We usually would write a frame axiom for a fluent, say On(A,Top(B)), block A is on the top of block B, and an action, in this case Shoot as,
![]()
However, since ![]() no longer encodes what events occurred, we
need to say something like, ``if no event that could change the fluent
On(A,Top(B)) occurred in the interval between s and s' and On(A,Top(B))
held at s then On(A,Top(B)) will hold at s'.'' It is notable that this
needs the notion of Changes that we introduced above. Thus we
write,
no longer encodes what events occurred, we
need to say something like, ``if no event that could change the fluent
On(A,Top(B)) occurred in the interval between s and s' and On(A,Top(B))
held at s then On(A,Top(B)) will hold at s'.'' It is notable that this
needs the notion of Changes that we introduced above. Thus we
write,
This will generate all of our frame axioms if we minimize Changes,
varying Succeeds and ![]() , and allowing the domain to vary as in
[Cos98b, Cos98a]. We do not consider using non-monotonic reasoning to
minimize Changes here, as we wish to stress other issues. Thus we
explicitly axiomatize the result of the minimization, much in the same
way as Reiter[Rei91] uses an explanation closure axiom and an
explicit statement of what events can change what fluents.
, and allowing the domain to vary as in
[Cos98b, Cos98a]. We do not consider using non-monotonic reasoning to
minimize Changes here, as we wish to stress other issues. Thus we
explicitly axiomatize the result of the minimization, much in the same
way as Reiter[Rei91] uses an explanation closure axiom and an
explicit statement of what events can change what fluents.