
Even frame axioms like this are not enough to allow us to carry out the simple reasoning we could carry out in previous versions of the situation calculus. We also need to know that certain events do not occur.
Consider the following example of moving a block. We have the action that moves a block, but to move a block successfully it must be clear. For instance if someone else puts another block on top of the block we are moving to, then our action will fail.
Thus our only effect axiom is the following one, which states moving block a onto block c succeeds, if a and c are clear for the entire duration, and a is not equal to c.

For this example we need some other facts about the world, these are given in an Appendix. We are also told that the only block that is not on the table is A, which is on B, and that the action of moving A to the top of C occurred at the situation S0.
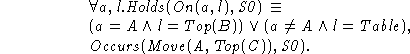
We can now write our frame axiom, which in this case is,
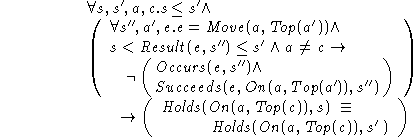
This states that a block a is on a block c in a situation s if and only if a is on c in s', so long as there is no event e, of moving moving a to Top(a'), which occurs, and is successful.
Some writers like to think that if an event that might change a fluent f occurs, but fails, then the fluent f should be undetermined. We can weaken our frame axiom, so that even if the event of moving a block a' to a fails, then our block a might not be clear. We write this as,
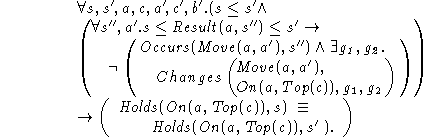
In general we shall prefer the stronger frame axiom.
We wish to prove that
![]()
however, we can only prove the weaker,
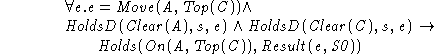
Thus, we need to prove that A and C remain clear during the move
action in order to show that the action is successful. To show that
they remain clear we need to use our frame axiom. But, all we can
prove is that the A block remains clear if there is no successful
move action ![]() that occurs, and whose
result is before
that occurs, and whose
result is before ![]() . As we allow situations
before S0, we can imagine that there was a move in progress that
placed a block on C just after S0.
. As we allow situations
before S0, we can imagine that there was a move in progress that
placed a block on C just after S0.
Thus we explicitly state that no action that might put something on
A or C occurred in the interval![]() , save of course the action of putting A on the top of
C.
, save of course the action of putting A on the top of
C.

We can now prove that
![]()
as the above principal allows us to prove that A and C are clear for the entire interval.
We cannot prove that C remains on the Table however, as there may be events that put C on top of other blocks. These events will not make C unclear, so they do not block the action of putting A on C. To prove that C remains on the table we would need,
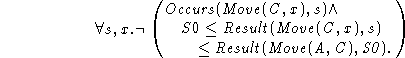
It is notable that there was no need to state that no other actions
occurred. It sufficed![]() to say that no other events occurred that might
cause a precondition of an event in our narrative to fail. The notion
that we need only state that certain events did not occur becomes very
important if we wish to axiomatize domains in a way that will later
allow them to be conjoined. In fact, the motivating property for
developing this new axiomatization was to allow separate
axiomatizations, that do not interfere with each other, to be
conjoined. This is not possible in the old-style situation calculus,
as we explicitly list the sequence of actions that occurs. It is also
not possible if we state that the only events that occur are those
mentioned, as is sometimes done in narrative reasoning.
to say that no other events occurred that might
cause a precondition of an event in our narrative to fail. The notion
that we need only state that certain events did not occur becomes very
important if we wish to axiomatize domains in a way that will later
allow them to be conjoined. In fact, the motivating property for
developing this new axiomatization was to allow separate
axiomatizations, that do not interfere with each other, to be
conjoined. This is not possible in the old-style situation calculus,
as we explicitly list the sequence of actions that occurs. It is also
not possible if we state that the only events that occur are those
mentioned, as is sometimes done in narrative reasoning.
The reasoning that we did was not significantly more difficult than the usual reasoning in the situation calculus. We needed to check a few more conditions, namely that blocks remained clear, but strategies, such as goal regression[Rei91] continue to be effective.