In this section 1 want to establish a relation between the use of recursive functions to define computations, the flow chart notation, and programs expressed as sequences of ALGOL-type assignment statements, together with conditional go to's. The latter we shall call Algolic programs with the idea of later extending the notation and methods of proof to cover more of the language of ALGOL. Remember that our purpose here is not to create yet another programming language, but to give tools for proving facts about programs.
In order to regard programs as recursive functions,
we shall define the state vector 
of a program at a given
time, to be the set of current assignments of values to the
variables of the program. In the case of a machine
language program, the state vector is the set of current
contents of those registers whose contents change
during the course of execution of the program.
When a block of program having a single entrance
and exit is executed, the effect of this execution on the
state vector may be described by a function 
giving the new state vector in terms of the old. Consider
a program described by the flow chart of fig. 1.
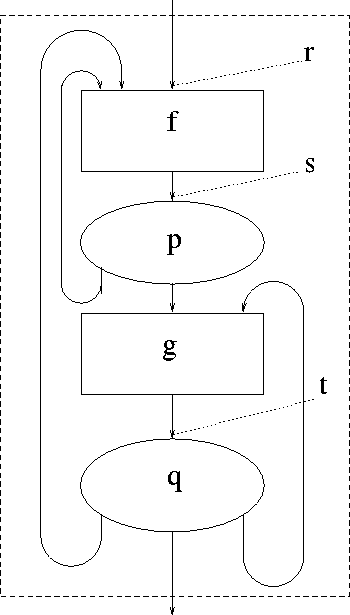
Fig. 1 Flow chart for equations shown below.
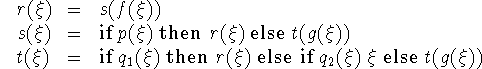
The two inner computation blocks are described by
functions 
and 
, telling how these blocks affect
the state vector. The decision ovals are described by
predicates 
, 
, and 
that give the conditions
for taking the various paths. We wish to describe the
function 
that gives the effect of the whole block,
in terms of the functions f and g and the predicates
p, 
, and 
. This is done with the help of two auxiliary
functions s and t. 
describes the change in between
the point labelled s in the chart and the final exit from
the block; t is defined similarly with respect to the
point labelled t. We can read the following equations
directly from the flow chart:
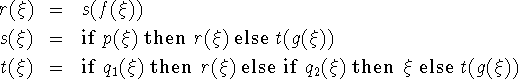
In fact, these equations contain exactly the same information as does the flow chart.
Consider the function mentioned earlier, given by
It corresponds, as we leave the reader to convince himself, to the Algolic program
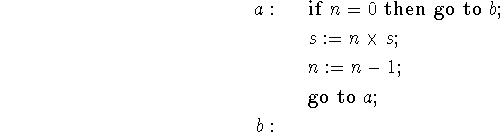
Its flow chart is given in fig. 2.
This flow chart is described by the function 
and the equation
where corresponds to the condition n=0, to
the statement n := n - 1, and to the statement
.
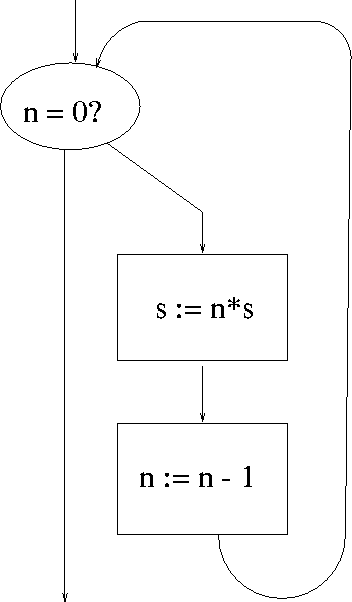
Fig. 2 Flow chart for as described by the
following equations.
where
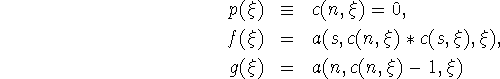
and so
We shall regard the state vector as having many
components, but the only components affected by the
present program are the s-component and the n-component.
In order to compute explicitly with the
state vectors, we introduce the function 
which
denotes the value assigned to the variable 
in the
state vector , and we also introduce the function
which denotes the state vector that results
when the value assigned to in is changed to
,
and the values of the other variables are left unchanged.
The predicates and functions of state vectors mentioned above then become:
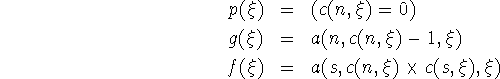
We can prove by recursion induction that
but in order to do so we must use the following facts about the basic state vector functions:
The proof parallels the previous proof that
but the formulae are longer.
While all flow charts correspond immediately to recursive functions of the state vector, the converse is not the case. The translation from recursive function to flow chart and hence to Algolic program is immediate, only if the recursion equations are in iterative form. Suppose we have a recursion equation
where 
is a conditional
expression defining the function r in terms of the
functions 
. 
is said to be in iterative form if r
never occurs as the argument of a function but only in
terms of the main conditional expression in the form
In the examples, all the recursive definitions except
are in interative form. In that one, (n - 1)! occurs as a term of a product. Non-iterative recursive functions translate into Algolic programs that use themselves recursively as procedures. Numerical calculations can usually be transformed into iterative form, but computations with symbolic expressions usually cannot, unless quantities playing the role of push-down lists are introduced explicitly.