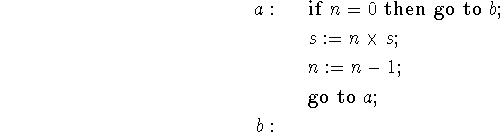
In this section we extend the principle of recursion induction so that it can be applied directly to Algolic programs without first transforming them to recursive functions. Consider the Algolic program
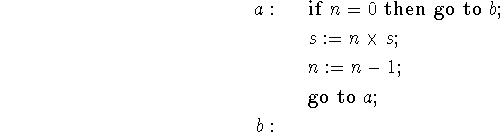
We want to prove it equivalent to the program

Before giving this proof we shall describe the principle of recursion induction as it applies to a simple class of flow charts. Suppose we have a block of program represented by fig. 3a. Suppose we have proved that this block is equivalent to the flow chart of fig. 3b where the shaded block is the original block again. This corresponds to the idea of a function satisfying a functional equation. We may now conclude that the block of fig. 3a is equivalent to the flow chart of fig. 3c for those state vectors for which the program does not get stuck in a loop in fig. 3c.
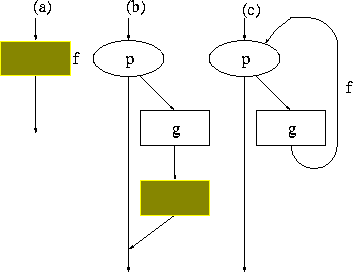
Fig. 3 Recursion induction applied to flow charts.
This can be seen as follows. Suppose that, for a particular input, the program of fig. 3c goes around the loop n times before it comes out. Consider the flow chart that results when the whole of fig. 3b is substituted for the shaded (or yellow) block, and then substituted into this figure again, etc. for a total of n substitutions. The state vector in going through this flow chart will undergo exactly the same tests and changes as it does in going through fig. 3c, and therefore will come out in n steps without ever going through the shaded (or yellow) block. Therefore, it must come out with the same value as in fig. 3c. Therefore, for any vectors for which the computation of fig. 3c converges, fig. 3a is equivalent to fig. 3c.
Thus, in order to use this principle to prove the equivalence of two blocks we prove that they satisfy the same relation, of type 3a-3b, and that the corresponding 3c converges.
We shall apply this method to showing that the two programs mentioned above are equivalent. The first program may be transformed as follows:
from
![]()
to
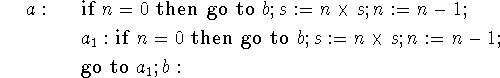
The operation used to transform the program is simply to write separately the first execution of a loop.
In the case of the second program we go:
from
![]()
to
![]()
to
![]()
to
![]()
The operations used here are: first, the introduction of a spurious branch, after which the same action is performed regardless of which way the branch goes; second, a simplification based on the fact that if the branch goes one way then n = 0, together with rewriting one of the right-hand sides of an assignment statement; and third, elimination of a label corresponding to a null statement, and what might be called an anti-simplification of a sequence of assignment statements. We have not yet worked out a set of formal rules justifying these steps, but the rules can be obtained from the rules given above for substitution, replacement and manipulation of conditional expressions.
The result of these transformations is to show that the two programs each satisfy a relation of the form: program is equivalent to
![]()
The program corresponding to fig. 3c in this case, is precisely the first program which we shall assume always converges. This completes the proof.