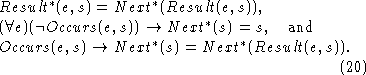 induction might be to
show that a block unmoved by each of a sequence of events is in the
same position in
induction might be to
show that a block unmoved by each of a sequence of events is in the
same position in 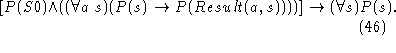 .
.
Several kinds of mathematical induction seem to be required. For
example, one may want to prove a proposition ![]() by showing
that it is true for s and is preserved by the events that occur
between s and
by showing
that it is true for s and is preserved by the events that occur
between s and ![]() . A related kind of induction is needed to
prove that something is true for all situations arising in the operation
of a buzzer. The simplest case of the
. A related kind of induction is needed to
prove that something is true for all situations arising in the operation
of a buzzer. The simplest case of the 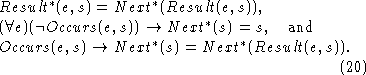 induction might be to
show that a block unmoved by each of a sequence of events is in the
same position in
induction might be to
show that a block unmoved by each of a sequence of events is in the
same position in 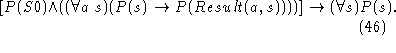 .
.
The simplest situation calculus is Reiter's [Rei01]. The formula is
Here are two formulas
(47) is appropriate when 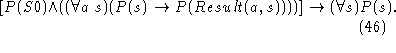 is defined.
is defined.
When 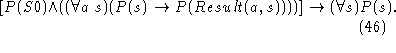 is not defined, as in the buzzer case, we can use
is not defined, as in the buzzer case, we can use
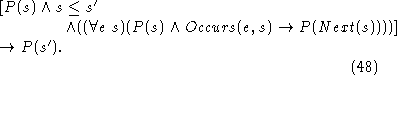 to mean that s' is a distant successor of s and have
the axiom.
to mean that s' is a distant successor of s and have
the axiom.