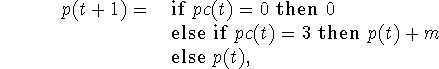
In Algol 48 we write this algorithm as a set of old fashioned recursion equations for three functions of time, namely p(t), i(t) and pc(t), where the first two correspond to the variables in the program, and pc(t) tells how the ``program counter'' changes. The only ideas that would have been unconventional in 1948 are the explicit use of a program counter and the conditional expressions. We have
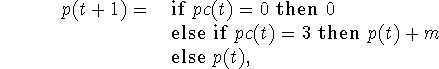
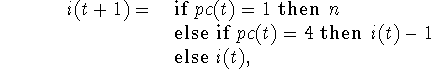
and
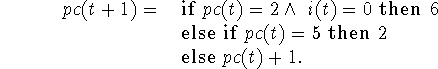
The correctness of the Algol 48 program is represented by the sentence
![]()
This sentence may be proved from the sentences representing the program supplemented by the axioms of arithmetic and the axiom schema of mathematical induction. No special theory of programming is required. The easiest proof uses mathematical induction on n applied to a formula involving p(t) = m(n-i(t)).
Algol 48 programs are organized quite differently from Algol 60 programs. Namely, the changes to variables are sorted by variable rather than sequentially by time.