Actions by Persons and Joint Actions of Groups

When there is more than one actor acting, we can consider three levels of complexity. The simplest level is when the actors act jointly to achive the goal. The second level is when one actor (or more than one) does something to motivate the others, e.g. one person pays another to do something. This generalizes to a hierarchy of influence. The hard level is when the actors have competing motivations and must negotiate or fight. This is the subject of game theory, and we won't pursue it in this article.

As MCP was originally formulated, the missionaries and cannibals are moved like pieces on a chessboard. Let's consider elaborations in which the actions of individual missionaries and cannibals are considered. One eventual goal might be to allow a formalization in which a cannibal has to be persuaded to row another cannibal across the river and bring the boat back. However, our discussion starts with simpler phenomena.

We now consider an action by a person as a particular kind of event. What we have written $Result(a,s)$ we now write $Result(Does(person,a),s)$. If there is only one person, nothing is gained by the expansion.

Consider a proposition $Can\mbox{-}Achieve(person,goal,s)$, meaning that the person $person$ can achieve the goal $goal$ starting from the situation $s$. For the time being we shall not say what goals are, because our present considerations are independent of that decision. The simplest case is that there is a sequence of actions $\{a_1,\ldots,a_n\}$ such that

$$Result(Does(person,a_n),Result(\ldots Result(Does(person,a_1),s)\ldots ))$$

satisfies $goal$.

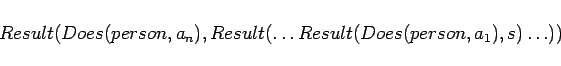
Now let's consider achievement by a group. We will say $Can\mbox{-}Achieve(group,goal,s)$ provided there is a sequence of events $\{Does(person_1,a_1),\ldots,Does(person_n,a_n)\}$, where each $person_i$ is in $group$, and the $person_i$s are not assumed to be distinct, and such that

$$Result(Does(person_n,a_n),Result(\ldots Result(Does(person_1,a_1),s)\ldots ))$$

satisfies $goal$.

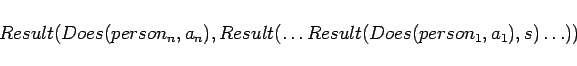
We can now introduce a simple notion of a person leading a group, written $leads(person,group)$ or more generally $leads(person,group,s)$. We want the axioms

$$leads(person,group) \land Can\mbox{-}Achieve(group,goal,s) \rightarrow Can\mbox{-}Achieve(person,s)$$

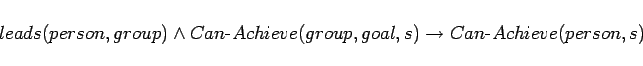
Thus a leader of a group can achieve whatever the group can achieve. Note that $person$ need not be a member of $group$ for this definition to work.

We could give the same definition for $leads(person,group,s)$, but maybe it would be better to make a definition that requires that $person$ maintain his leadership of $group$ in the succeeding situations.

$Leads(person,group)$ is too strong a statement in general, because the members of a group only accept leadership in some activities.