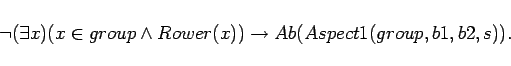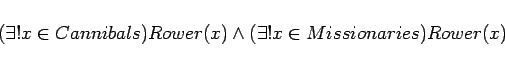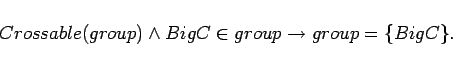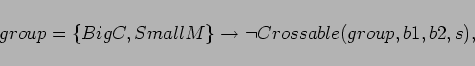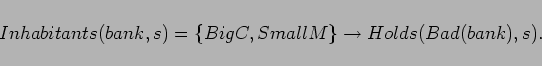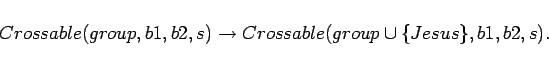- The boat is a rowboat. (Or the boat is a motorboat). By
itself this is a trivial elaboration. Adding it should not affect
the reasoning. By default, a tool, i.e. the boat, is usable.
Further elaborations might use specific properties of rowboats.
- The missionaries and cannibals have hats, all
different--another trivial elaboration. These hats may be
exchanged among the missionaries and cannibals. In all the
elaborations mentioned below, exchanging hats is an action
irrelevant to crossing the river. There are two demands on the
reasoner. Epistemologically, whatever reasoning that establishes
a plan for crossing the river without the hats should be valid
with the hats. This includes any nonmonotonic reasoning.
Heuristically, the problem may not be trivial. Why should it be
obvious that exchanging hats is of no use? Certainly we can make
elaborations in which it is of use, e.g. we can assert that if the
smallest missionary wears the hat belonging to the largest
missionary, the largest cannibal won't eat him even if they go
together.
However, it should be possible to tell a problem solver: Look for
a solution that has no hat change actions. After that, the
reasoner should find the solution as easily as it would if hats
were never mentioned.
- There are four missionaries and four cannibals. The problem
is now unsolvable. In ordinary logic, adding sentences that there
are four of each produces a contradiction. Belief revision
systems ought to make the correct change. It seems to me that
people take a metalinguistic stance, just saying ``Change the
numbers of missionaries and cannibals to four'', thus regarding
the original statement of the problem as an object. Actually what
is regarded as an object is the sense of the original statement,
since people ordinarily don't remember the words used.
Proofs of impossibility take the following form. Choose a
predicate formula 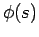 on situations. Show
on situations. Show 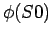 and
and
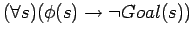 . Also show
. Also show
Thus you can't get out of the situations satisfying 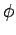 , and
the goal isn't included. The simplest
, and
the goal isn't included. The simplest 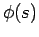 is a disjunction
of specific locations of the missionaries and cannibals in the
reachable situations, but this disjunction is long, and it is very
likely possible to do better.
is a disjunction
of specific locations of the missionaries and cannibals in the
reachable situations, but this disjunction is long, and it is very
likely possible to do better.
We can regard the argument that four can't cross as a kind of
elaboration. A formalism that doesn't permit expressing the
best argument is then deficient in elaboration tolerance.
- The boat can carry three. Four can cross but not five. If
the boat can carry four an arbitrary number can cross. [2003 Sept:
This is mistaken. Joohyung Lee showed that if the boat holds
three, five can cross.]
- There is an oar on each bank. One person can cross in the
boat with just one oar, but two oars are needed if the boat is to
carry two people. We can send a cannibal to get the oar and then
we are reduced to the original problem. 4
A formalism using preconditions can accept this elaboration as
just adding a precondition for rowing, the action of putting an
oar in the boat and adding facts about the locations of the oars
in 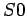 .
.
The oar-on-each-bank elaboration can be expressed by conjoining to
(12),
but this looks a bit ad hoc. In particular, it wouldn't
tolerate the further elaboration of making the boat hold three if
that elaboration were expressed as the single sentence
In order to admit the reasoning that getting the
oar reduces the problem to MCP0, we will need a notion of one
problem reducing to another--or one theory reducing to another.
- Only one missionary and one cannibal can row. The problem is
still solvable. Before this elaboration, we did not need to
distinguish among the missionaries or among the cannibals. An
elaboration tolerant language must permit this as an addition.
We use
|
(12) |
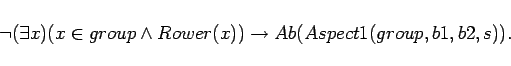 |
and
|
(13) |
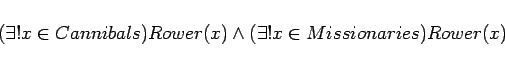 |
- The missionaries can't row. This makes the problem
impossible, since any solution requires two missionaries in the
boat at some time. The formalism must admit the statement and
proof of this lemma.
For this we need (12) and
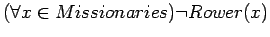 .
.
- The biggest cannibal cannot fit in the boat with another
person. The problem is solvable. However, if the
biggest missionary cannot fit in the boat with another
person the problem becomes unsolvable. We can imagine having to
elaborated in the direction of saying what sets of people can fit
in the boat. The elaborations are
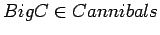 and
and
|
(14) |
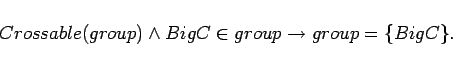 |
Note that the defining property of the biggest cannibal is
unnecessary to make the elaboration work. I assume we'd pay for
this shortcut, were further elaboration necessary.
The corresponding elaboration about the biggest missionary is
formalized in the same way; only the conclusion is different.
- If the biggest cannibal is isolated with the smallest
missionary, the latter will be eaten. A solution to the basic
problem can be specialized to avoid this contingency. We have the
Gricean implicature that the cannibals aren't all the same size,
and need to have language for referring to an individual as the
biggest cannibal and not just language to refer to him by name. We
have
|
(15) |
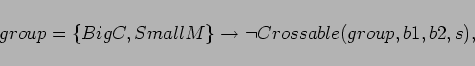 |
and
|
(16) |
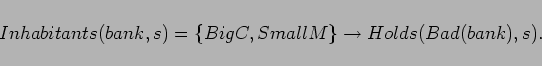 |
- One of the missionaries is Jesus Christ. Four can cross.
Here we are using cultural literacy. However, a human will not
have had to have read Mark 6:48-49 to have heard of
Jesus walking on water. The formalism of Section
6 permits this elaboration just by adjoining the
sentence
|
(17) |
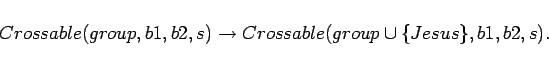 |
However, this elaboration says nothing about walking on water and
therefore seems to be a cheat.
- Three missionaries alone with a cannibal can convert him into
a missionary. The problem for elaboration tolerance is to change
a predicate that doesn't depend on situation or time to one that
does. Note that a sorted logical language with missionaries and
cannibals as distinct sorts would freeze the intolerance into the
language itself.
- The probability is 1/10 that a cannibal alone in a boat will
steal it. We can ask what is the probability that a given plan
will succeed, say the Amarel plan. The formalism of
[McC79a] treats propositions as objects. Using
that formalism
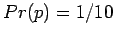 can be expressed for any proposition
can be expressed for any proposition
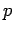 . I see at least two problems. The language of propositions
as objects needs to be rich enough to express notions like the
probability of a cannibal stealing the boat on an occasion--or of
being a thief who always steals boats if alone. The second
problem is that we need to be able to assert independence or joint
distributions without letting the entire formalism be taken over
by its probabilistic aspects. In MCP0, cannibals have to be alone
in the boat several times. We can write a formula that states
that probabilities are independent by default.
. I see at least two problems. The language of propositions
as objects needs to be rich enough to express notions like the
probability of a cannibal stealing the boat on an occasion--or of
being a thief who always steals boats if alone. The second
problem is that we need to be able to assert independence or joint
distributions without letting the entire formalism be taken over
by its probabilistic aspects. In MCP0, cannibals have to be alone
in the boat several times. We can write a formula that states
that probabilities are independent by default.
We now need to infer that the probability of successfully
completing the task is 0.9.
- There is a bridge. This makes it obvious to a
person that any number can cross provided two people can cross at
once. It should also be an obvious inductive argument in the
sense of McAllester [McA]. This is a straightforward
elaboration in situation calculus formalisms, since adding the
bridge is accomplished just by adding sentences. There is no need
to get rid of the boat unless this is part of the elaboration
wanted.
- The boat leaks and must be bailed concurrently with rowing.
Elaboration tolerance requires that treating a concurrent action
be a small change in the statement of the problem, and this will
show the limitations of some versions of situation calculus.
- The boat may suffer damage and have to be taken back to the
left bank for repair. This may happen at any time. This requires
that the formalism permit splitting the event of crossing the
river into two parts.
- There is an island. Then any number can cross, but showing
it requires inductive arguments. Though inductive, these
arguments should be obvious.
Defining the three stages--moving the cannibals to the island,
moving the missionaries to the opposite bank and then moving the
cannibals to the opposite bank--is an easy three step problem,
provided moving the sets of missionaries and cannibals can be
regarded as tasks. Whether the elaboration is easy depends on the
original representation.
There may be a nonmonotonic rule that if you keep getting
closer to a goal and there is no inferrable obstacle you will
achieve the goal. Zeno's ``paradox'' of Achilles and the
tortoise involves noting that this rule doesn't always
hold, i.e. is nonmonotonic. Such a rule would make the above
induction easy and maybe obvious.
- There are four cannibals and four missionaries, but if the
strongest of the missionaries rows fast enough, the cannibals won't
have gotten so hungry that they will eat the missionaries. This
could be made precise in various ways, but the information is
usable even in vague form.5
- There are four missionaries and four cannibals, but the
cannibals are not hungry initially, and the missionaries have a
limited amount of cannibal food. They can tell if a cannibal is
hungrier than he was and can avoid trouble by giving the food to
the cannibal who has got hungrier. This requires comparing a
situation and a successor situation.
- There are two sets of missionaries and
cannibals too far apart along the river to interact. The two
problem should be solvable separately without considering
interleaving actions at the two sites. If the two problems are
different elaborations, the work required and the length of the
proof should be the sum of the lengths for the separate problems
plus a small constant.
The theory of two sets of missionaries should be a
conservative extension of each of the subtheories. We have
called this property conjunctivity.
There are 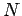 sites along the river with identical conditions. The
reasoning should be able to do one site, or a generalized site, and,
with a constant amount of additional reasoning, say that all
sites along the river with identical conditions. The
reasoning should be able to do one site, or a generalized site, and,
with a constant amount of additional reasoning, say that all 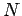 crossings are the same.
crossings are the same.
- After rowing twice, a person becomes too tired to row any more.
[Added 2003 April 1].
![]() on situations. Show
on situations. Show ![]() and
and
![]() . Also show
. Also show
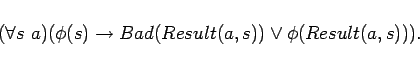
![]() .
.
![\begin{displaymath}
\begin{array}[l]{l}
Card(group) > Card(\{x\vert Oar(x) \lan...
...),s)\}) \\
\rightarrow Ab(Aspect1(group,b1,b2,s)),
\end{array}\end{displaymath}](img92.png)
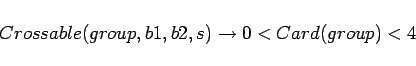
![]() .
.
![]() sites along the river with identical conditions. The
reasoning should be able to do one site, or a generalized site, and,
with a constant amount of additional reasoning, say that all
sites along the river with identical conditions. The
reasoning should be able to do one site, or a generalized site, and,
with a constant amount of additional reasoning, say that all ![]() crossings are the same.
crossings are the same.