Formalizing the Amarel Representation

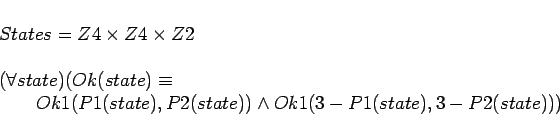
We use logic and set theory to formalize MCP0 and call the formalization MCP0a. In this formalization we are not concerned with elaboration tolerance. My opinion is that set theory needs to be used freely in logical AI in order to get enough expressiveness. The designers of problem-solving programs will just have to face up to the difficulties this gives for them.

$$\begin{array}{l} States = Z4 \times Z4 \times Z2 \\ \quad ... ...(state)) \land Ok1(3 - P1(state),3-P2(state))) \\ \end{array}$$

Here $Z2 = \{0,1\}$ and $Z4 = \{0,1,2,3\}$ are standard set-theory names for the first two and the first four natural numbers respectively, and $P1$, $P2$ and $P3$ are the projections on the components of the cartesian product $Z4 \times Z4 \times Z2$.

Note that having used $3 - P1(state)$ for the number of missionaries on the other bank put information into posing the problem that is really part of solving it, i.e. it uses a law of conservation of missionaries.

$$\begin{array}{l} (\forall m\ c)(Ok1(m,c) \equiv m \in Z4 \l... ... \\ Moves = \{(1,0),(2,0),(0,1),(0,2),(1,1)\} \\ \end{array}$$

$$\begin{array}{rl} (\forall move\ state)\quad&\\ (Result(mo... ...(2P3(state)-1)P2(move), \\ &1 - P3(state))), \\ \end{array}$$

where $Mkstate(m,c,b)$ is the element of $States$ with the three given components.

$$(\forall s1\ s2)( Step(s1,s2) \equiv (\exists move)(s2 = Result(move,s1) \land Ok(s2)))$$

$$Attainable1 = Transitive\mbox{-}closure(Step)$$

$$Attainable(s) \equiv s = (3,3,1) \lor Attainable1((3,3,1),s)$$

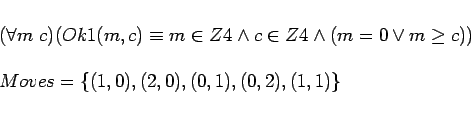
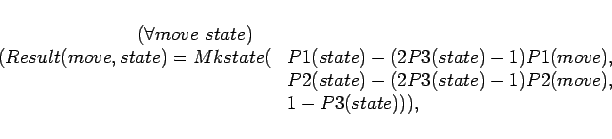
Notice that all the above sentences are definitions, so there is no question of the existence of the required sets, functions, constants and relations. The existence of the transitive closure of a relation defined on a set is a theorem of set theory. No fact about the real world is assumed, i.e. nothing about rivers, people, boats or even about actions.

From these we can prove

$$attainable((0,0,0)).$$

The applicability of MCP0a to MCP must be done by postulating a correspondence between states of the missionaries and cannibals problem and states of MCP0a and then showing that actions in MCP have suitable corresponding actions in MCP0a. We will postpone this until we have a suitable elaboration tolerant formalization of MCP.

MCP0a has very little elaboration tolerance, in a large measure because of fixing the state space in the axioms. Situation calculus will be more elaboration tolerant, because the notation doesn't fix the set of all situations.