


Next: Formalizing the Amarel Representation
Up: ELABORATION TOLERANCE
Previous: Nonmonotonic reasoning
A Typology of Elaborations
There are many kinds of elaborations a person can tolerate, and they
pose different problems to different logical formalizations. Here are
some kinds of elaborations.
- irrelevant actors, actions and objects
- Sentences establishing
the existence of such entities should not vitiate the reasoning
leading to a solution.
- adding preconditions, actions, effects of actions and objects
- The example of the oars adds a precondition to rowing and adds the
action of picking up the oars. Several situation calculus and event
calculus formalisms allow this--assuming sentences are added before
the nonmonotonic reasoning is done. Tolerating added preconditions
is a criterion for good solutions of the qualification problem, and
tolerating adding effects relates similarly to the ramification
problem.
- changing a parameter
- This is needed when the numbers of
missionaries and cannibals are changed from 3 to 4. In English,
this is accomplished by an added sentence. Doing it that way in logic
requires a suitable belief revision method as part of the
basic logical formalism. At present we must use minor brain surgery
to replace certain occurrences of the number 3.
- making a property situation dependent
- Whether
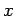 is a
missionary is not situation dependent in MCP0, but we can elaborate
to a missionary becoming a cannibal. It is tempting to say that all
properties should be situation dependent from the beginning, and
such a formalism would admit this elaboration easily. I think this
might lead to an infinite regress, but I can't formulate the problem
yet.
is a
missionary is not situation dependent in MCP0, but we can elaborate
to a missionary becoming a cannibal. It is tempting to say that all
properties should be situation dependent from the beginning, and
such a formalism would admit this elaboration easily. I think this
might lead to an infinite regress, but I can't formulate the problem
yet.
- specialization
- In one situation calculus formalization we have
the action
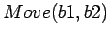 . If there are guaranteed to be exactly two
places, we can replace this action by
. If there are guaranteed to be exactly two
places, we can replace this action by 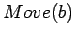 , regarding this as
, regarding this as
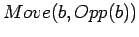 , where
, where 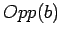 designates the opposite bank and
satisfies
designates the opposite bank and
satisfies
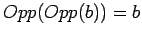 . We regard this kind of specialization
as an easy kind of elaboration.
. We regard this kind of specialization
as an easy kind of elaboration.
- generalization
- Some of our elaborations can be composed of an
generalization of the language--replacing a function by a function of
more arguments, e.g. making whether a person is a cannibal or
missionary situation dependent or replacing going from a bank
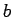 to
the opposite bank
to
the opposite bank 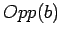 by going from
by going from 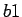 to
to 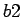 . Many
elaborations consist of a generalization followed by the addition of
sentences, e.g. adding preconditions or effects to an action.
. Many
elaborations consist of a generalization followed by the addition of
sentences, e.g. adding preconditions or effects to an action.
- unabbreviation
- This is a particular case of generalization.
Suppose we write
![$(\forall a \in
Actions)Abbreviates[a,Does(person,a)]$](img14.png) . We mean to use it in
elaborating
. We mean to use it in
elaborating 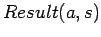 to
to
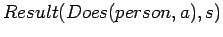 in sentences
where it is somehow clear which person is referred to. The square
brackets mean that this is a metalinguistic statement, but I don't
presently understand precisely how unabbreviation is to work.
in sentences
where it is somehow clear which person is referred to. The square
brackets mean that this is a metalinguistic statement, but I don't
presently understand precisely how unabbreviation is to work.
- going into detail
- An event like the action of crossing the
river is made up of subactions. However, the relation between an
event and its subevents is not often like the relation between a
program and its subroutines, because asserting that the action
occurs does not imply specific subactions. Rowing is a detail of
crossing a river when rowboats are used, but rowing is not a part of
the general notion of crossing a river.. Bailing if necessary is
another detail. Getting oars or a bailing can are associated
details. There is more about this apparently controversial point in
[McC95].
- m...s and c...s as actors
- MCP and almost all of the
elaborations we have considered take a god-like view of the actions,
e.g. we send a cannibal to get an oar. We can also elaborate in the
direction of supposing that the actions of cannibals and
missionaries are sometimes determined by the situation. In this
case, it may be convenient to use a predicate
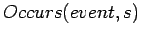 and
let one possible event be
and
let one possible event be
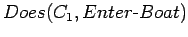 . The
situation calculus treatment has to be altered and looks more like
event calculus.
. The
situation calculus treatment has to be altered and looks more like
event calculus.
- simple parallel actions
- If one of the missionaries is Jesus
Christ, we can transport 4 missionaries and 4 cannibals. We get 3
cannibals on the far bank and one on the initial bank. Then two
ordinary missionaries and Jesus cross, the ordinaries in the boat
and Jesus walking on water. The rest of the solution is
essentially the same as in MCP0. A missionary and a cannibal
row back and now the remaining two missionaries cross. We then send
a cannibal to ferry the remaining two cannibals. We haven't tackled
the problem of being able to say ``essentially the same'' in logic.
The formalization must permit Jesus to cross in parallel with the
other missionaries so that the missionaries are never outnumbered.
This isn't the same as having Jesus cross as a separate action.
- full parallelism
- This is what permits requiring that the boat
be bailed.
- events other than actions
- The simple
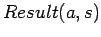 doesn't
allow for events other than actions. To handle them we have used
[McC95] a predicate
doesn't
allow for events other than actions. To handle them we have used
[McC95] a predicate 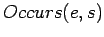 asserting that the event
asserting that the event 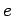 occurs in the situation
occurs in the situation 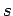 . Then
. Then 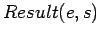 can be used.
can be used.
- comparing different situations
- This works ok in situation
calculus, but some other formalisms don't allow it or make it
awkward. Thus we can have
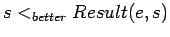 to say that
the situation is better after event
to say that
the situation is better after event 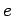 occurs. We may also want
occurs. We may also want
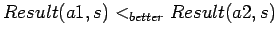 , comparing the result of
doing
, comparing the result of
doing 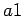 with the result of doing
with the result of doing 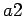 .
.
- splitting an entity
- Sometimes an entity, e.g. a node in a
graphy, an edge, or a concept needs to be split into two entities of
the same type so that separate properties can be assigned to each
subentity. Thus we may split cannibals into strong and weak
cannibals.
- continuous time and discrete time
- If Achilles runs enough
faster than the tortoise, there is a time when Achilles catches up.
We use the fluent
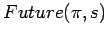 to assert that the situation
to assert that the situation 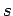 will be followed in the future by a situation satisfying
will be followed in the future by a situation satisfying 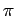 . We
do not require formalizing real numbers to express the Achilles
catching up sentence
. We
do not require formalizing real numbers to express the Achilles
catching up sentence



Next: Formalizing the Amarel Representation
Up: ELABORATION TOLERANCE
Previous: Nonmonotonic reasoning
John McCarthy
2003-09-29
![\begin{displaymath}
\begin{array}[l]{l}
Future((\lambda s)
(Value(Distance\mb...
...stance\mbox{-}covered\mbox{-}by(Tortoise),s)),
S0).
\end{array}\end{displaymath}](img29.png)
![\begin{displaymath}
\begin{array}[l]{l}
Future((\lambda s)
(Value(Distance\mb...
...stance\mbox{-}covered\mbox{-}by(Tortoise),s)),
S0).
\end{array}\end{displaymath}](img29.png)