
This approach can be seen to be similar to modeling systems with structured equations [Simon, 1953] [Druzdel and Simon, 1994], or Bayesian networks [Balke and Pearl, 1994b] [Balke and Pearl, 1994a] [Pearl, 1995]. Rather than have equations that give the value of a variable, we have arbitrary propositions. The dependency relationships are captured by the frame, rather than links. In our model, exogenous variables are in the frame, as are the functions that give the value of the other variables. Updating the Bayes net can then be seen to be updating the frame.
One major difference between our approach and structural equation models or Bayesian networks is that we consider arbitrary propositions, and consider these relative to a background approximate theory. This approximate theory can be rich, that is, not completely describable. The other major difference is that Bayesian networks focus on the probability distribution of certain variables, rather than on facts in general.
We now briefly sketch Galles's and Pearl's formalization of causal models, their generalization of structural equations.

We now show how to represent causal model as a cartesian frame.
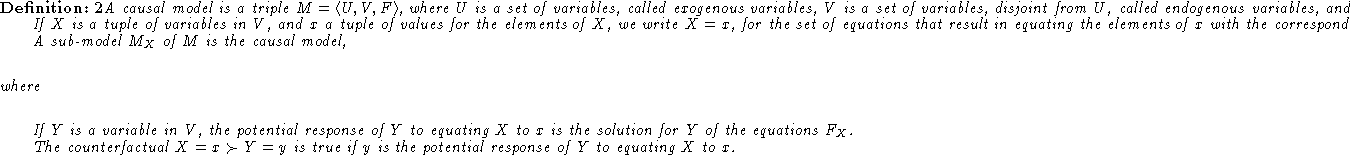
We now show that ![]() is true in a causal model M if
and only if
is true in a causal model M if
and only if ![]() is true in the cartesian frame
is true in the cartesian frame ![]() ,
with current world
,
with current world ![]() .
.
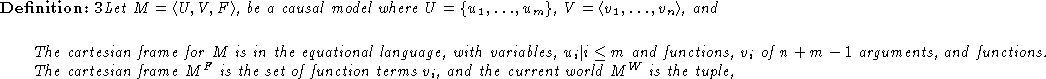
Proof: We prove this by showing that the equations in sub-model
![]() are exactly the formulas encoded by the result of updating the
state vector
are exactly the formulas encoded by the result of updating the
state vector ![]() by each element of X = x.
by each element of X = x.
The sub-model ![]() is the causal model,
is the causal model,
where
The formulas encoded by ![]() are
are
The formulas encoded by the sequence of assignments is
To show this, it is enough to realize that no ![]() can appear twice
in X, and thus every distinct update updates a distinct variable.
can appear twice
in X, and thus every distinct update updates a distinct variable.
Thus the equations in sub-model ![]() is exactly the formulas encoded.
Finally, the conditions for y being a potential response of Y to
equating X to x are exactly the conditions for Y = y following
from the equations,
is exactly the formulas encoded.
Finally, the conditions for y being a potential response of Y to
equating X to x are exactly the conditions for Y = y following
from the equations,
height6pt width4pt depth0pt