In this section we show that we can derive facts that do not contain counterfactual implications from counterfactuals.
We take as our theory, the axioms in Section 5, save for the last
axiom 
. From the counterfactual,
we derive that, .
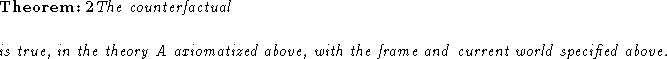
Proof: We first note that in A, the co-ordinates have the values, 
. We expand the definition of a counterfactual being true,
namely,
to get, by replacing the function c everywhere its value at that argument,
This is a meta-theoretic statement, so we
translate this into second order logic, by quantifying over
predicates, functions and objects in the standard way
.
where 
is the tuple of all constant symbols in the language, and 
is a tuple of variables, equal in type and arity to the constants in , we write variables in Z' as 
etc.
This second order sentence captures the truth of the counterfactual.
We can conjoin this with the other axioms in the theory A, and ask
whether it implies, in second order logic.
It does, as can be seen from instantiating the universally quantified
variables, with their corresponding constants, except for 
and which are instantiated by the predicate P true of the
smallest set of situations satisfying the formulas below, and the
partial function, 
,
defined from P,
The result of instantiating these terms, and noting that the left hand side is derivable from the theory A gives the sentence.
However, we also have 
, and the axiom,
Instantiating this with 
and simplifying gives 
. As we know by domain closure that
we have
as required. 