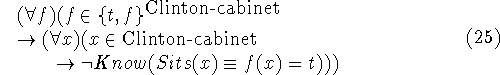
Relative consistency provides a reasonable way of handling single cases of non-knowledge. However, we may want more. For example, suppose we want to say that we know nothing about whether any member of Clinton's cabinet is standing or sitting except (for example) that none of them sits when Clinton is standing in the same room.
The theory should then have lots of models, and we can parameterize them by a set of the standees that is arbitary except for the above condition. Here's a formula using non-knowledge.
but this only tells us that for each member of the cabinet, we don't know whether he is sitting.
We want the stronger formula
which asserts that for all we know, Clinton's cabinet could be standing or sitting in an arbitrary pattern. Here we have had to take a quantifier inside the Know function. [McCarthy, 1979b] discusses difficulties in formalizing this and doesn't offer a satisfactory solution.
[McCarthy, 1999] gives a simple way of parameterizing the set of models of a propositional sentence. However, there can be no neat way of parameterizing the models of an arbitary first order theory. Thus parameterizing the set of axioms for group theory would amount to parameterizing the set of all groups, and group theory tells us that there is no straightforward parameterization.