Mental events, especially mental actions

Mental events change the situation just as do physical events.

Here is a list of some mental events, mostly described informally.

• In the simplest formalisms mental events occur sequentially. This corresponds ot a stream of consciousness. Whether or not the idea describes human consciousness, it is a design option for robot consciousness.
• Learn(p). The robot learns the fact p. An obvious consequence is

   

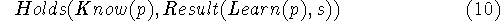
  provided the effects are definite enough to justify the Result formalism. More likely we'll want something like

   

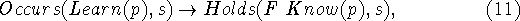
  where Occurs(event,s) is a point fluent asserting that event occurs (instantaneously) in situation s. F(p) is the proposition that the proposition p will be true at some time in the future. The temporal function F is used in conjunction with the function next and the axiom

   

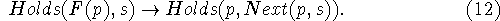
  Here Next(p,s) denotes the next situation following s in which p holds. (12) asserts that if F(p) holds in s, then there is a next situation in which p holds. (This Next is not the Next operator used in some temporal logic formalisms.)

• The robot learning p has an effect on the rest of its knowledge. We are not yet ready to propose one of the many belief revision systems for this. Indeed we don't assume logical closure.
• What about an event Forget(p)? Forgetting p is definitely not an event with a definite result. What we can say is

   

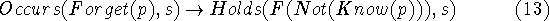
  In general, we shall want to treat forgetting as a side-effect of some more complex event. Suppose Foo is the more complex event. We'll have

   

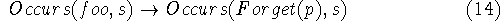
• The robot may decide to do action a. This has the property:

   

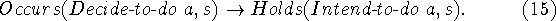
  The distinction is that Decide is an event, and we often don't need to reason about how long it takes. 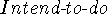is a fluent that persists until something changes it. Some call these point fluents and continuous fluents respectively.

• The robot may decide to assume p, e.g. for the sake of argument. The effect of this action is not exactly to believe p, but rather involves entering a context Assume(c,p) in which p holds. This formalism is described in [McCarthy, 1993] and [McCarthy and Buvac, 1998].
• The robot may infer p from other sentences, either by deduction or by some nonmonotonic form of inference.
• The robot may see some object. One result of seeing an object may be knowing that it saw the object. So we might have

   

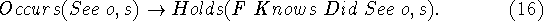
  Formalizing other effects of seeing an object require a theory of seeing that is beyond the scope of this article.

It should be obvious to the reader that we are far from having a comprehensive list of the effects of mental events. However, I hope it is also apparent that the effects of a great variety of mental events on the mental part of a situation can be formalized. Moreover, it should be clear that useful robots will need to observe mental events and reason with facts about their effects.

Most work in logical AI has involve theories in which it can be shown that a sequence of actions will achieve a goal. There are recent extensions to concurrent action, continuous action and strategies of action. All this work applies to mental actions as well.

Mostly outside this work is reasoning leading to the conclusion that a goal cannot be achieved. Similar reasoning is involved in showing that actions are safe in the sense that a certain catastrophe cannot occur. Deriving both kinds of conclusion involves inductively inferring quantified propositions, e.g. ``whatever I do the goal won't be achieved'' or ``whatever happens the catastrophe will be avoided.'' This is hard for today's automated reasoning techniques, but Reiter [Reiter, 1993] and his colleagues have made important progress.