The uses of logic in AI and other parts of computer science
that have been undertaken so far do not involve such an extensive
collection of concepts. However, it seems to me that reaching human
level AI will involve all of the following--and probably more.
- Logical AI
- Logical AI in the sense of the present article was
proposed in [McC59]
and also in [McC89]. The
idea is that an agent can represent knowledge of its world, its goals and
the current situation by sentences in logic and decide what to
do by inferring that a certain action or course of action is
appropriate to achieve its goals.
Logic is also used in weaker ways in AI, databases, logic
programming, hardware design and other parts of computer science.
Many AI systems represent facts by a limited subset of logic and use
non-logical programs as well as logical inference to make
inferences. Databases often use only ground formulas. Logic
programming restricts its representation to Horn clauses. Hardware
design usually involves only propositional logic. These
restrictions are almost always justified by considerations of
computational efficiency.
- Epistemology and Heuristics
- In philosophy, epistemology is
the study of knowledge, its form and limitations. This will do
pretty well for AI also, provided we include in the study common
sense knowledge of the world and scientific knowledge. Both of
these offer difficulties philosophers haven't studied, e.g. they
haven't studied in detail what people or machines can know about
the shape of an object the field of view, remembered from previously
being in the field of view, remembered from a description or
remembered from having been felt with the hands. This is
discussed a little in [MH69].
Most AI work has concerned heuristics, i.e. the algorithms that
solve problems, usually taking for granted a particular epistemology
of a particular domain, e.g. the representation of chess positions.
- Bounded Informatic Situation
- Formal theories in the physical
sciences deal with a bounded informatic situation. Scientists
decide informally in advance what phenomena to take into account.
For example, much celestial mechanics is done within the Newtonian
gravitational theory and does not take into account possible
additional effects such as outgassing from a comet or
electromagnetic forces exerted by the solar wind. If more phenomena
are to be considered, scientists must make a new theories--and of
course they do.
Most AI formalisms also work only in a bounded informatic situation.
What phenomena to take into account is decided by a person before the
formal theory is constructed. With such restrictions, much of the
reasoning can be monotonic, but such systems cannot reach human
level ability. For that, the machine will have to decide for
itself what information is relevant, and that reasoning will
inevitably be partly nonmonotonic.
One example is the ``blocks world'' where the position of a block
x is entirely characterized by a sentence At(x,l) or On(x,y),
where l is a location or y is another block.
Another example is the Mycin [DS77] expert system in which the
ontology (objects considered) includes diseases, symptoms, and
drugs, but not patients (there is only one), doctors or events
occurring in time. See [McC83] for more comment.
- Common Sense Knowledge of the World
- As first discussed in
[McC59], humans have a lot of knowledge of the world which
cannot be put in the form of precise theories. Though the
information is imprecise, we believe it can still be put in logical
form. The Cyc project [LG90] aims at making a large
base of common sense knowledge. Cyc is useful, but further progress
in logical AI is needed for Cyc to reach its full potential.
- Common Sense Informatic Situation
- In general a thinking human
is in what we call the common sense informatic situation, as
distinct from the bounded informatic situation. The known
facts are necessarily incomplete. We live in a world of
middle-sized object which can only be partly observed. We only
partly know how the objects that can be observed are built from
elementary particles in general, and our information is even more
incomplete about the structure of particular objects. These
limitations apply to any buildable machines, so the problem is not
just one of human limitations.

In many actual situations, there is no a priori limitation
on what facts are relevant. It may not even be clear in advance
what phenomena should be taken into account. The consequences of
actions cannot be fully determined. The common sense
informatic situation necessitates the use of approximate
concepts that cannot be fully defined and the use of
approximate theories involving them. It also requires
nonmonotonic reasoning in reaching conclusions. Many AI
texts assume that the information situation is bounded--without even
mentioning the assumption explicitly.
The common sense informatic situation often includes some knowledge about
the system's mental state as discussed in [McC96a].
One key problem in formalizing the common sense informatic situation
is to make the axiom sets elaboration
tolerant.
- Epistemologically Adequate Languages
- A logical language for use
in the common sense informatic situation must be capable of
expressing directly the information actually available to agents.
For example, giving the density and temperature of air and its
velocity field and the Navier-Stokes equations does not practically
allow expressing what a person or robot actually can know about the
wind that is blowing. We and robots can talk about its direction,
strength and gustiness approximately, and can give a few of these
quantitities numerical values with the aid of instruments if
instruments are available, but we have to deal with the phenomena
even when no numbers can be obtained. The idea of epistemological
adequacy was introduced in [MH69].
- Robot
- We can generalize the notion of a robot as a system with
a variant of the physical capabilities of a person, including the
ability to move around, manipulate objects and perceive scenes, all
controlled by a computer program. More generally, a robot is a
computer-controlled system that can explore and manipulate an
environment that is not part of the robot itself and is, in some
important sense, larger than the robot. A robot should maintain a
continued existence and not reset itself to a standard state after
each task. From this point of view, we can have a robot that
explores and manipulates the Internet without it needing legs, hands
and eyes. The considerations of this article that mention robots
are intended to apply to this more general notion. The internet
robots discussed so far are very limited in their mentalities.
- Qualitative Reasoning
- This concerns reasoning about physical
processes when the numerical relations required for applying
the formulas of physics are not known. Most of the work in
the area assumes that information about what processes to take
into account are provided by the user. Systems that must be
given this information often won't do human level qualitative
reasoning. See [De90] and [Kui94].
- Common Sense Physics
- Corresponds to people's ability to make
decisions involving physical phenomena in daily life, e.g. deciding
that the spill of a cup of hot coffee is likely to burn Mr. A, but
Mr. B is far enough to be safe. It differs from qualitative
physics, as studied by most researchers in qualitative
reasoning, in that the system doing
the reasoning must itself use common sense knowledge to decide what
phenomena are relevant in the particular case. See [Hay85]
for one view of this.
- Expert Systems
- These are designed by people, i.e. not by
computer programs, to take a limited set of phenomena into account.
Many of them do their reasoning using logic, and others use
formalisms amounting to subsets of first order logic. Many require
very little common sense knowledge and reasoning ability.
Restricting expressiveness of the representation of facts
is often done to increase computational efficiency.
- Knowledge Level
- Allen Newell ([New82] and
[New93]) did not advocate (as we do here) using logic as the
way a system should represent its knowledge internally. He did say
that a system can often be appropriately described as knowing
certain facts even when the facts are not represented by sentences
in memory. This view corresponds to Daniel Dennett's
intentional stance [Den71], reprinted in
[Den78], and was also proposed and elaborated in
[McC79].
- Elaboration Tolerance
- A set of facts described as a logical
theory needs to be modifiable by adding sentences rather than only
by going back to natural language and starting over. For example,
we can modify the missionaries and cannibals problem by saying that
there is an oar on each bank of the river and that the boat can be
propelled with one oar carrying one person but needs two oars to
carry two people. Some formalizations require complete rewriting to
accomodate this elaboration. Others share with natural language the
ability to allow the elaboration by an addition to what was
previously said.
There are degrees of elaboration tolerance. A state space
formalization of the missionaries and cannibals problem in which a
state is represented by a triplet 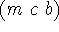 of the numbers of
missionaries, cannibals and boats on the initial bank is less
elaboration tolerant than a situation calculus formalism in which
the set of objects present in a situation is not specified in
advance. In particular, the former representation needs surgery to
add the oars, whereas the latter can handle it by adjoining more
sentences--as can a person. The realization of elaboration
tolerance requires nonmonotonic reasoning. See [McC97].
of the numbers of
missionaries, cannibals and boats on the initial bank is less
elaboration tolerant than a situation calculus formalism in which
the set of objects present in a situation is not specified in
advance. In particular, the former representation needs surgery to
add the oars, whereas the latter can handle it by adjoining more
sentences--as can a person. The realization of elaboration
tolerance requires nonmonotonic reasoning. See [McC97].
- Robotic Free Will
- Robots need to consider their choices and
decide which of them leads to the most favorable situation. In
doing this, the robot considers a system in which its own outputs
are regarded as free variables, i.e. it doesn't consider the process
by which it is deciding what to do. The perception of having
choices is also what humans consider as free will. The
matter is discussed in [MH69] and is roughly in accordance
with the philosophical attitude towards free will called
compatibilism, i.e. the view that determinism and free will
are compatible.
- Reification
- To refify an entity is to ``make a thing''
out of it (from Latin re for thing). From a
logical point of view, things are what variables can range over.
Logical AI needs to reify hopes, intentions and ``things wrong
with the boat''. Some philosophers deplore reification, referring
to a ``bloated ontology'', but AI needs more things than are dreamed
of in the philosophers' philosophy. In general, reification gives a
language more expressive power, because it permits referring to
entities directly that were previously mentionable only in a
metalanguage.
- Ontology
- In philosophy, ontology is the branch that studies
what things exist. W.V.O. Quine's view is that the ontology is what
the variables range over. Ontology has been used variously in AI,
but I think Quine's usage is best for AI. ``Reification'' and
``ontology'' treat the same phenomena. Regrettably, the word
``ontology'' has become popular in AI in much vaguer senses.
Ontology and reification are basically the same concept.
- Approximate Concepts
- Common sense thinking cannot avoid
concepts without clear definitions. Consider the welfare of an
animal. Over a period of minutes, the welfare is fairly well
defined, but asking what will benefit a newly hatched chick over the
next year is ill defined. The exact snow, ice and rock that
constitutes Mount Everest is ill defined. The key fact about
approximate concepts is that while they are not well defined,
sentences involving them may be quite well defined. For example,
the proposition that Mount Everest was first climbed in 1953 is
definite, and its definiteness is not compromised by the
ill-definedness of the exact boundaries of the mountain.
See [McC99b].
There are two ways of regarding approximate concepts. The first is
to suppose that there is a precise concept, but it is incompletely
known. Thus we may suppose that there is a truth of the matter as
to which rocks and ice constitute Mount Everest. If this approach
is taken, we simply need weak axioms telling what we do know but not
defining the concept completely.
The second approach is to regard the concept as intrinsically
approximate. There is no truth of the matter. One practical
difference is that we would not expect two geographers independently
researching Mount Everest to define the same boundary. They would
have to interact, because the boundaries of Mount Everest are yet to
be defined.
- Approximate Theories
- Any theory involving approximate concepts
is an approximate theory. We can have a theory of the welfare of
chickens. However, its notions don't make sense if pushed too far.
For example, animal rights people assign some rights to chickens but
cannot define them precisely. It is not presently apparent whether
the expression of approximate theories in mathematical logical
languages will require any innovations in mathematical logic. See
[McC99b].
- Ambiguity Tolerance
- Assertions often turn out to be ambiguous
with the ambiguity only being discovered many years after the
assertion was enunciated. For example, it is a priori
ambiguous whether the phrase ``conspiring to assault a Federal
official'' covers the case when the criminals mistakenly believe
their intended victim is a Federal official. An ambiguity in a law
does not invalidate it in the cases where it can be considered
unambiguous. Even where it is formally ambiguous, it is subject to
judicial interpretation. AI systems will also require means of
isolating ambiguities and also contradictions. The default rule is
that the concept is not ambiguous in the particular case. The
ambiguous theories are a kind of approximate theory.
- Causal Reasoning
- A major concern of logical AI has been
treating the consequences of actions and other events. The
epistemological problem concerns what can be known about the
laws that determine the results of events. A theory of causality is
pretty sure to be approximate.
- Situation Calculus
- Situation calculus is the most studied
formalism for doing causal reasoning. A situation is in principle a
snapshot of the world at an instant. One never knows a
situation--one only knows facts about a situation. Events occur in
situations and give rise to new situations. There are many variants
of situation calculus, and none of them has come to dominate.
[MH69] introduces situation calculus. [GLR91] is a
1991 discussion.
- Fluents
- Functions of situations in situation calculus. The
simplest fluents are propositional and have truth values. There are
also fluents with values in numerical or symbolic domains.
Situational fluents take on situations as values.
- Frame Problem
- This is the problem of how to express the facts
about the effects of actions and other events in such a way that it
is not necessary to explicitly state for every event, the fluents it
does not affect. Murray Shanahan [Sha97] has an extensive
discussion.
- Qualification Problem
- This concerns how to express the
preconditions for actions and other events. That it is necessary to
have a ticket to fly on a commercial airplane is rather
unproblematical to express. That it is necessary to be wearing
clothes needs to be kept inexplicit unless it somehow comes up.
- Ramification Problem
- Events often have other effects than those
we are immediately inclined to put in the axioms concerned with the
particular kind of event.
- Projection
- Given information about a situation, and axioms
about the effects of actions and other events, the projection
problem is to determine facts about future situations. It is
assumed that no facts are available about future situations other
than what can be inferred from the ``known laws of motion'' and what
is known about the initial situation. Query: how does one tell a
reasoning system that the facts are such that it should rely on
projection for information about the future.
- Planning
- The largest single domain for logical AI has been
planning, usually the restricted problem of finding a finite
sequence of actions that will achieve a goal. [Gre69a] is the
first paper to use a theorem prover to do planning. Planning is
somewhat the inverse problem to projection.
- Narrative
- A narrative tells what happened, but any narrative
can only tell a certain amount. What narratives can tell, how to
express that logically, and how to elaborate narratives is given a
preliminary logical treatment in [McC95b] and
more fully in [CM98a].
[PR93] and [RM94] are relevant here.
A narrative will usually give facts about the future of a situation
that are not just consequences of projection from an initial
situation. [While we may suppose that the future is entirely
determined by the initial situation, our knowledge doesn't permit
inferring all the facts about it by projection. Therefore,
narratives give facts about the future beyond what follows by
projection.]
- Understanding
- A rather demanding notion is most useful. In particular,
fish do not understand swimming, because they can't use knowledge to
improve their swimming, to wish for better fins, or to teach other
fish. See the section on understanding
in [McC96a]. Maybe fish do learn to improve their swimming,
but this presumably consists primarily of the adjustment of
parameters and isn't usefully called understanding. I would apply
understanding only to some systems that can do hypothetical
reasoning--if p were true, then q would be true. Thus Fortran
compilers don't understand Fortran.
- Consciousness, awareness and introspection
- Human level AI systems
will require these qualities in order to do tasks we assign them. In
order to decide how well it is doing, a robot will need to be
able to examine its goal structure and the structure of its beliefs
from the outside. See [McC96a].
- Intention to do something
- Intentions as objects are discussed
briefly in [McC89] and [McC96a].
- Mental situation calculus
- The idea is that there are mental
situations, mental fluents and mental events that give rise to new
mental situations. The mental events include observations and
inferences but also the results of observing the mental situation up
to the current time. This allows drawing the conclusion that there
isn't yet information needed to solve a certain problem, and
therefore more information must be sought outside the robot or
organism. [SL93] treats this and
so does [McC96a].
- Discrete processes
- Causal reasoning is simplest when applied to
processes in which discrete events occur and have definite results.
In situation calculus, the formulas s' = result(e,s) gives the new
situation s' that results when the event e occurs in situation
s. Many continuous processes that occur in human or robot
activity can have approximate theories that are discrete.
- Continuous Processes
- Humans approximate continuous processes
with representations that are as discrete as possible. For example,
``Junior read a book while on the airplane from Glasgow to London.''
Continuous processes can be treated in the situation calculus, but
the theory is so far less successful than in discrete cases. We
also sometimes approximate discrete processes by continuous ones.
[Mil96] and [Rei96] treat this problem.
- Non-deterministic events
- Situation calculus and other causal
formalisms are harder to use when the effects of an action are
indefinite. Often result(e,s) is not usefully axiomatizable and
something like occurs(e,s) must be used.
- Concurrrent Events
- Formalisms treating actions and other events
must allow for any level of dependence between events. Complete
independence is a limiting case and is treated in
[McC95b].
- Conjunctivity
- It often happens that two phenomena are
independent. In that case, we may form a description of their
combination by taking the conjunction of the descriptions of the
separate phenomena. The description language satisfies
conjunctivity if the conclusions we can draw about one of the
phenomena from the combined description are the same as the
conjunctions we could draw from the single description. For
example, we may have separate descriptions of the assassination of
Abraham Lincoln and of Mendel's contemporaneous experiments with
peas. What we can infer about Mendel's experiments from the
conjunction should ordinarily be the same as what we can infer from
just the description of Mendel's experiments. Many formalisms for
concurrent events don't have this property, but conjunctivity
itself is applicable to more than concurrent events.
To use logician's language, the conjunction of the two theories
should be a conservative extension of each of the theories.
Actually, we may settle for less. We only require that the
inferrable sentences about Mendel (or about Lincoln) in the
conjunction are the same. The combined theory may admit inferring
other sentences in the language of the separate theory that weren't
inferrable in the separate theories.
- Learning
- Making computers learn presents two
problems--epistemological and heuristic. The
epistemological problem is to define the space of concepts that the
program can learn. The heuristic problem is the actual learning
algorithm. The heuristic problem of algorithms for learning has
been much studied and the epistemological mostly ignored. The
designer of the learning system makes the program operate with a
fixed and limited set of concepts. Learning programs will never
reach human level of generality as long as this approach is
followed. [McC59] says, ``A computer can't learn what
it can't be told.'' We might correct this, as suggested by Murray
Shanahan, to say that it can only learn what can be expressed in the
language we equip it with. To learn many important concepts, it
must have more than a set of weights. [MR94] and
[BM95] present some progress on learning within a logical
language. The many kinds of learning discussed in [Mit97]
are all, with the possible exception of inductive logic programming,
very limited in what they can represent--and hence can conceivably
learn. [McC99a] presents a challenge to machine learning
problems and discovery programs to learn or discovery the reality
behind appearance.
- Representation of Physical Objects
- We aren't close to having
an epistemologically adequate language for this. What do I know
about my pocket knife that permits me to recognize it in my pocket
or by sight or to open its blades by feel or by feel and sight?
What can I tell others about that knife that will let them recognize
it by feel, and what information must a robot have in order to pick
my pocket of it?
- Representation of Space and Shape
- We again have the problem of
an epistemologically adequate representation. Trying to match what
a human can remember and reason about when out of sight of the scene
is more what we need than some pixel by pixel representation. Some
problems of this are discussed in [McC95a] which
concerns the Lemmings computer games. One can think about a
particular game and decide how to solve it away from the display of
the position, and this obviously requires a compact representation
of partial information about a scene.
- Discrimination, Recognition and Description
-
Discrimination is the deciding which category a stimulus
belongs to among a fixed set of categories, e.g. decide which
letter of the alphabet is depicted in an image. Recognition
involves deciding whether a stimulus belongs to the same set, i.e.
represents the same object, e.g. a person, as a previously seen
stimulus. Description involves describing an object in
detail appropriate to performing some action with it, e.g. picking
it up by the handle or some other designated part. Description is
the most ambitious of these operations and has been the forte of
logic-based approaches.
- Logical Robot
- [McC59] proposed that a
robot be controlled by a program that infers logically that a
certain action will advance its goals and then does that action.
This approach was implemented in [Gre69b], but the program
was very slow. Shortly greater speed was obtained in systems like
STRIPS at the cost of limiting the generality of facts the robot
takes into account. See [Nil84], [LRL
 97], and
[Sha96].
97], and
[Sha96].
- Declarative Expression of Heuristics
- [McC59] proposes
reasoning be controlled by domain-dependent and problem-dependent
heuristics expressed declaratively. Expressing heuristics
declaratively means that a sentence about a heuristic can be the
result of reasoning and not merely something put in from the outside
by a person. Josefina Sierra [Sie98b], [Sie98a],
[Sie98c], [Sie99] has made some recent progress.
- Logic programming
- Logic programming isolates a
subdomain of first order logic that has nice computational
properties. When the facts are described as a logic program,
problems can often be solved by a standard program, e.g. a Prolog
interpreter, using these facts as a program. Unfortunately, in
general the facts about a domain and the problems we would like
computers to solve have that form only in special cases.
- Useful Counterfactuals
- ``If another car had come over the hill
when you passed that Mercedes, there would have been a head-on
collision.'' One's reaction to believing that counterfactual
conditional sentence is quite different from one's reaction to the
corresponding material conditional. Machines need to represent such
sentences in order to learn from not-quite-experiences.
See [CM98b].
- Formalized Contexts
- Any particular bit of thinking occurs in
some context. Humans often specialize the context to particular
situations or theories, and this makes the reasoning more definite,
sometimes completely definite. Going the other way, we sometimes
have to generalize the context of our thoughts to take some
phenomena into account.
It has been worthwhile to admit contexts as objects into the
ontology of logical AI. The prototype formula ist(c,p) asserts
that the proposition p is true in the context c. The formal
theory is discussed in [McC93], [MB98] and in papers
by Sasa Buvac, available in [Buv95].
- Rich and Poor Entities
- A rich entity is one about which
a person or machine can never learn all the facts. The state of the
reader's body is a rich entity. The actual history of my going home
this evening is a rich entity, e.g. it includes the exact position
of my body on foot and in the car at each moment. While a system
can never fully describe a rich entity, it can learn facts about it
and represent them by logical sentences.
Poor entities occur in plans and formal theories and in
accounts of situations and events and can be fully prescribed. For
example, my plan for going home this evening is a poor entity, since
it does not contain more than a small, fixed amount of detail. Rich
entities are often approximated by poor entities. Indeed some rich
entities may be regarded as inverse limits of trees of poor
entities. (The mathematical notion of inverse limit may or may not
turn out to be useful, although I wouldn't advise anyone to study the
subject quite yet just for its possible AI applications.)
- Nonmonotonic Reasoning
- Both humans and machines must draw
conclusions that are true in the ``best'' models of the facts
being taken into account. Several concepts of best are used
in different systems. Many are based on minimizing something. When
new facts are added, some of the previous conclusions may no longer
hold. This is why the reasoning that reached these conclusions is
called nonmonotonic.
- Probabilistic Reasoning
- Probabilistic reasoning is a kind
of nonmonotonic reasoning. If the probability of one sentence is
changed, say given the value 1, other sentences that previously had
high probability may now have low or even 0 probability. Setting up
the probabilistic models, i.e defining the sample space of
``events'' to which probabilities are to be given often involves
more general nonmonotonic reasoning, but this is conventionally done
by a person informally rather than by a computer.
In the open common sense informatic situation, there isn't any
apparent overall sample space. Probabilistic theories may formed by
limiting the space of events considered and then establishing a
distribution. Limiting the events considered should be done by
whatever nonmonotonic reasoning techniques are developed techniques
for limiting the phenomena taken into account. (You may take this
as a confession that I don't know these techniques.) In forming
distributions, there would seem to be a default rule that two events
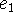 and
and 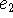 are to be taken as independent unless there is a
reason to do otherwise.
are to be taken as independent unless there is a
reason to do otherwise. 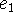 and
and 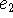 can't be just any events
but have to be in some sense basic events.
can't be just any events
but have to be in some sense basic events.
- Circumscription
- A method of nonmonotonic reasoning involving
minimizing predicates (and sometimes domains). It was introduced in
[McC77], [McC80] and [McC86]. An up-to-date
discussion, including numerous variants, is [Lif94].
- Default Logic
- A method of nonmonotonic reasoning
introduced in [Rei80] that is the main survivor along with
circumscription.
- Yale Shooting Problem
- This problem, introduced in
[HM86], is a simple Drosophila for nonmonotonic
reasoning. The simplest formalizations of causal reasoning using
circumscription or default logic for doing the nonmonotonic
reasoning do not give the result that intuition demands. Various
more recent formalizations of events handle the problem ok. The
Yale shooting problem is likely to remain a benchmark problem for
formalizations of causality.
- Design Stance
- Daniel Dennett's idea [Den78] is to
regard an entity in terms of its function rather than in terms of
its physical structure. For example, a traveller using a hotel
alarm clock need not notice whether the clock is controlled by a
mechanical escapement, the 60 cycle power line or by an internal
crystal. We formalize it in terms of (a) the fact that it can be
used to wake the traveller, and (b) setting it and the noise it
makes at the time for which it is set.
- Physical Stance
- We consider an object in terms of its physical
structure. This is needed for actually building it or repairing it
but is often unnecessary in making decisions about how to use it.
- Intentional Stance
- Dennett proposes that sometimes we consider
the behavior of a person, animal or machine by ascribing to it
belief, desires and intentions. This is discussed in
[Den71] and [Den78] and also in [McC79].
- Relation between logic and calculation and various data
structures
-
Murray Shanahan recommends putting in something about this.
- Creativity
- Humans are sometimes creative--perhaps rarely in
the life of an individual and among people. What is creativity? We
consider creativity as an aspect of the solution to a problem rather
than as attribute of a person (or computer program).
A creative solution to a problem contains a concept not present in
the functions and predicates in terms of which the problem is posed.
[McC64] and [McC]discuss the mutilated checkerboard
problem.
The problem is to determine whether a checkerboard with two
diagonally opposite squares can be removed can be covered with
dominoes, each of which covers two rectilinearly adjacent squares.
The standard proof that this can't be done is creative
relative to the statement of the problem. It notes that a domino
covers two squares of opposite color, but there are 32 squares of
one color and 30 of the other color to be colored.
Colors are not mentioned in the statement of the problem, and their
introduction is a creative step relative to this statement. For a
mathematician of moderate experience (and for many other people),
this bit of creativity is not difficult. We must, therefore,
separate the concept of creativity from the concept of difficulty.
Before we can have creativity we must have some
elaboration tolerance.
Namely, in the simple languagge of A tough nut  , the
colors of the squares cannot even be expressed. A program confined
to this language could not even be told the solution. As discussed
in [McC96b], Zermelo-Frankel set theory is an adequate
language. In general, set theory, in a form allowing definitions
may have enough elaboration tolerance in general. Regard this as a
conjecture that requires more study.
, the
colors of the squares cannot even be expressed. A program confined
to this language could not even be told the solution. As discussed
in [McC96b], Zermelo-Frankel set theory is an adequate
language. In general, set theory, in a form allowing definitions
may have enough elaboration tolerance in general. Regard this as a
conjecture that requires more study.
- How it happened
- Consider an action like buying a pack of
cigarettes on a particular occasion and the subactions thereof. It
would be a mistake to regard the relation between the action and
its subactions as like that between a program and its subroutines.
On one occasion I might have bought the cigarettes from a machine.
on a second occasion at a supermarket, and on a third occasion from
a cigarettelegger, cigarettes having become illegal.
![]() of the numbers of
missionaries, cannibals and boats on the initial bank is less
elaboration tolerant than a situation calculus formalism in which
the set of objects present in a situation is not specified in
advance. In particular, the former representation needs surgery to
add the oars, whereas the latter can handle it by adjoining more
sentences--as can a person. The realization of elaboration
tolerance requires nonmonotonic reasoning. See [McC97].
of the numbers of
missionaries, cannibals and boats on the initial bank is less
elaboration tolerant than a situation calculus formalism in which
the set of objects present in a situation is not specified in
advance. In particular, the former representation needs surgery to
add the oars, whereas the latter can handle it by adjoining more
sentences--as can a person. The realization of elaboration
tolerance requires nonmonotonic reasoning. See [McC97].
![]()
![]() and
and ![]() are to be taken as independent unless there is a
reason to do otherwise.
are to be taken as independent unless there is a
reason to do otherwise. ![]() and
and ![]() can't be just any events
but have to be in some sense basic events.
can't be just any events
but have to be in some sense basic events.
![]() , the
colors of the squares cannot even be expressed. A program confined
to this language could not even be told the solution. As discussed
in [McC96b], Zermelo-Frankel set theory is an adequate
language. In general, set theory, in a form allowing definitions
may have enough elaboration tolerance in general. Regard this as a
conjecture that requires more study.
, the
colors of the squares cannot even be expressed. A program confined
to this language could not even be told the solution. As discussed
in [McC96b], Zermelo-Frankel set theory is an adequate
language. In general, set theory, in a form allowing definitions
may have enough elaboration tolerance in general. Regard this as a
conjecture that requires more study.