Kempe (or perhaps someone still earlier)
noticed that countries with three or fewer neighbors present
no problem. No matter how the rest of the map is colored, there is always
a color available for such a country.
We use this in to improve a Pereira-Porto map coloring program by
``reducing the map'' by
removing such countries and doing our trial-and-error coloring on the
reduced map, confident that once the reduced map is colored, the coloring
can be extended to the omitted countries.
The idea is even more powerful, because eliminating countries with three or fewer neighbors may remove enough neighbors from some other countries so that they have three or fewer neighbors and can themselves be removed. Therefore, the reduction process should be continued until a completely reduced map is obtained in which all countries have at least four neighbors. The maps of the states of the U.S. and the countries of Europe, Asia, Africa and South America all reduce to null maps when countries with three or fewer neighbors are successively eliminated
Likewise the map of Figure 1 reduces to the empty map. Thus we may remove country 4 with two neighbors and country 5 with three neigbors. This leaves all the remaining countries with three or fewer neighbors, so the second cycle of reduction leaves the null map, reduced map. Therefore, when we colored in the reverse order 1, 2, 3, 6, 4, 5, each country is colored without changing the color of any previously colored country.
If the programmer performs this reduction before he writes the goal statement, he will write
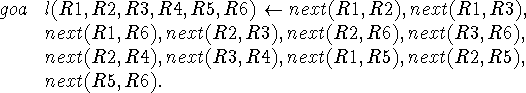
This PROLOG program will run with only the most local backtracking. Namely, after R1 has been chosen arbitrarily, several values will have to be tried for each of the variables R1, R2, R3, R6, R4, and R5, but once a value has been found that is compatible with the previously determined variables, it won't have to be changed again.
The new PROLOG program is logically equivalent to the previous program because it is just a rearrangement of the literals of a conjunction. However, the programmer has done the control. The interesting question is whether the reduction can be expressed in some way that can be regarded as adding control to the original logic, i.e., without changing the original logic.