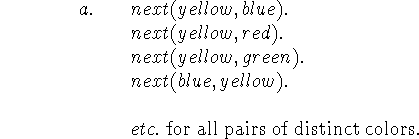
There are two parts. The first expresses that the adjacent countries must have different colors by listing the pairs of colors that may be adjacent. We have
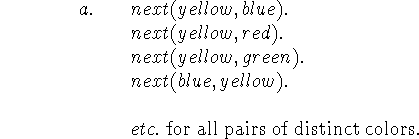
The remaining PROLOG statement is distinct for each map. For the map of Figure 1, which they use as an example, it is
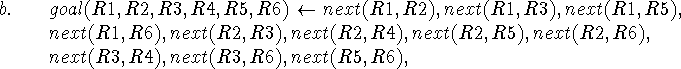
where each literal expresses the fact that a particular pair of adjacent regions must be compatibly colored.
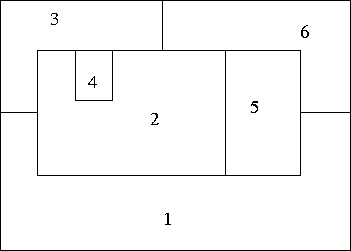
Figure 1.
Pereira and Porto give a trace of the execution of the program by standard depth first PROLOG. They point out that when an attempt to satisfy a literal fails, because the two adjacent regions mentioned have been assigned the same color, standard PROLOG will take back the most recent assignment of a color even if the region most recently colored was neither of those involved in the incompatibility. Their intelligent backtracking will change the color of one of the regions giving the incompatibility.
An outsider to logic programming may react unsympathetically and comment that this is just one more example of a logic programming system, with its standard way of doing searches, tripping over its own feet. However, we should also recall that brief and easy statement of the PROLOG program for the coloring and not give up this virtue without a fight.
Nevertheless, ``intelligent backtracking'' doesn't make (a) and (b) into a good coloring program. Indeed we shall argue that it doesn't even do full justice to the logic of the program. To see this we need two ideas of Kempe.