Here is an annotated EKL proof that circumscribes the predicate e(x,y) discussed in section 6.
![]()
What the user types is indicated by the numbered statements in lower case. What EKL types is preceded by semicolons at the beginning of each line and is in upper case. We omit EKL's type-out when it merely repeats what the command asked it to do, as in the commands DERIVE, ASSUME and DEFINE.
![]()
Since EKL does not have attachments to determine the equivalence of names, we establish a correspondence between the names in our domain and some natural numbers.
![]()
EKL does know about the distinctness of natural numbers, so this can be derived.
![]()
We have to tell EKL to use the properties of equality rather than regarding it as just another predicate symbol in order to do the next step. Sometimes this leads to combinatorial explosion.
![]()
This shows that two names themselves are distinct.
![]()
Here we use second order logic to define the notion of equivalence relation. The first word after ``define'' is the entity being defined and included between vertical bars is the defining relation. EKL checks that an entity satisfying the relation exists.
![]()
We define ax as a predicate we want our imitation equality to satisfy. We have chosen a very simple case, namely making a and b ``equal'' and nothing else.
![]()
This defines ax1 as the second order predicate specifying the circumscription of ax.
![]()
We now specify that e0 satisfies ax1. It takes till step 17 to determine what e0 actually is. When EKL includes circumscription as an operator, we may be able to write something like circumscribe(e0,ax1) and make this step occur. For now it's just an ordinary assumption.
![]()
The predicate e2 defined here is what e0 will turn out to be.
![]()
Now EKL agrees that e2 is an equivalence relation. This step takes the KL-10 about 14 seconds.
![]()
Moreover it satisfies ax.
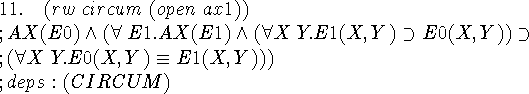
A trivial step of expanding the definition of ax1. EKL tells us that this fact depends on the assumption CIRCUM. So do many of the subsequent lines of the proof, but we omit it henceforth to save space.
![]()
The first conjunct of the previous step.
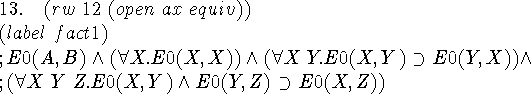
We expand ax(e0) according to the definitions of ax and equiv.
![]()
This is a fact of propositional calculus used as a rewrite rule in the next step. A program that can use circumscription by itself will either need to generate this step or systematically avoid the need for it.
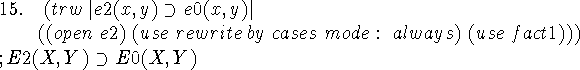
This is the least obvious step, because rewrite by cases is used after some preliminary transformation of the formula.
![]()
DERIVE is substituting e2 for the variable e1 in step 11 and using
the fact ax(e2) and step 15 to infer the conclusion of the implication
that follows the quantifier ![]()
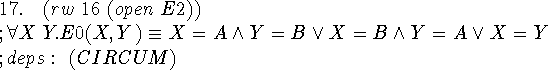
Expanding the definition of e2 tells us the final result of circumscribing e0(x,y). A more complex ax(e0) -- see step 5 -- would give a more complex result upon circumscription. However, it seems that the proof would be similar. Therefore, it could perhaps be made into some kind of macro.