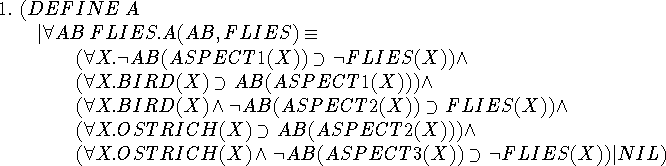
At present there are no reasoning or problem-solving programs using circumscription. A first step towards such a program involves determining what kinds of reasoning are required to use circumscription effectively. As a step towards this we include in this and the following appendix two proofs in EKL (Ketonen and Weening 1984), an interactive theorem prover for the theory of types. The first does the bird problem and the second a simple unique names problem. It will be seen that the proofs make substantial use of EKL's ability to admit arguments in second order logic.
Each EKL step begins with a command given by the user. This is usually followed by the sentence resulting from the step in a group of lines each ending in a semicolon, but this is omitted for definitions when the information is contained in the command. We follow each step by a brief explanation. Of course, the reader may skip this proof if he is sufficiently clear about what steps are involved. However, I found that pushing the proof through EKL clarified my ideas considerably as well as turning up bugs in my axioms.
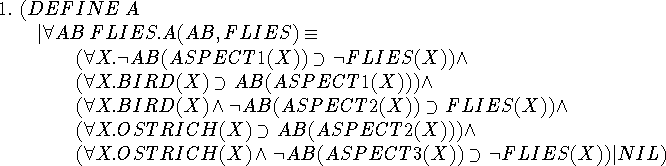
This defines the second order predicate A(ab,flies), where ab and flies are predicate variables. Included here are the specific facts about flying being taken into account.
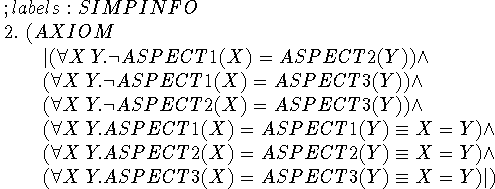
These facts about the distinctness of aspects are used in step 20 only. Since axiom 2 is labelled SIMPINFO, the EKL simplifier uses it as appropriate when it is asked to simplify a formula.
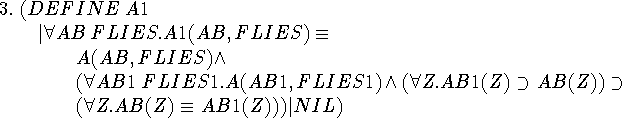
This is the circumscription formula itself.
![]()
Since EKL cannot be asked (yet) to do a circumscription, we assume the result. Most subsequent statements list line 4 as a dependency. This is appropriate since circumscription is a rule of conjecture rather than a rule of inference.
![]()
This definition and the next say what we are going to substitute for the bound predicate variables.
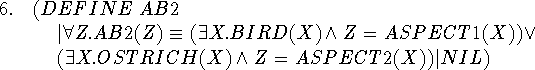
The fact that this definition is necessarily somewhat awkward makes for some difficulty throughout the proof.
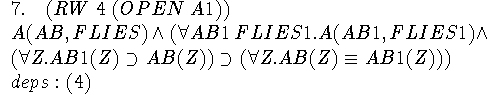
This step merely expands out the circumscription formula. RW stands for ``rewrite a line'', in this case line 4.
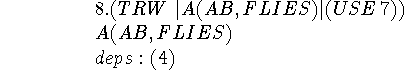
We separate the two conjuncts of 7 in this and the next step.
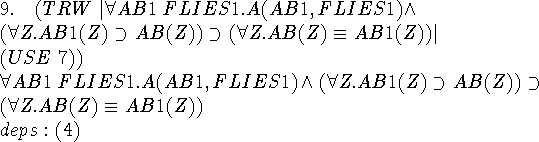
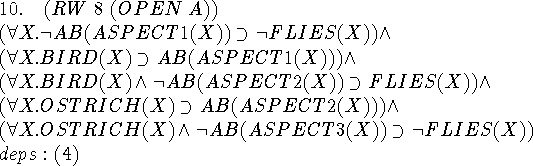
Expanding out the axiom using the definition a in step 1.
![]()
Our goal is step 15, but we need to assume its premiss and then derive its conclusion.
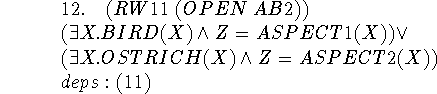
We use the definition of ab.
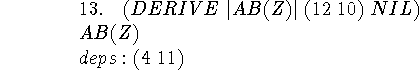
This is our first use of EKL's DERIVE command. It is based on the notion of direct proof of (Ketonen and Weyhrauch 1984). Sometimes it can do rather complicated things in one step.
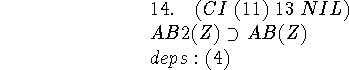
We discharge the assumption 11 with the ``conditional introduction'' command.
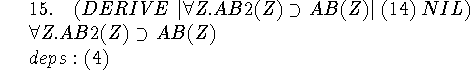
Universal generalization.

This is another rather lengthy computation, but it tells us that ab2 and flies2 satisfy the axioms for ab and flies.

Now we substitute ab2 and flies2 in the definition of A and get a result we can compare with step 16.
![]()
We have shown that ab2 and flies2 satisfy A.
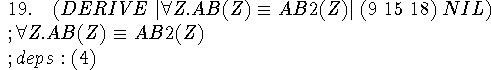
9 was the circumscription formula, and 15 and 18 are its two premisses, so we can now derive its conclusion. Now we know exactly what entities are abnormal.
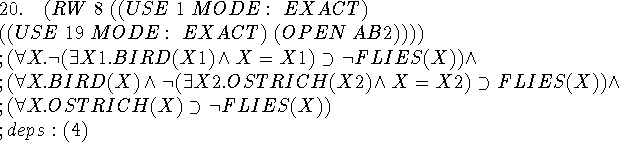
We rewrite the axiom now that we know what's abnormal. This gives a somewhat awkward formula that nevertheless contains the desired conclusion. The occurrences of equality are left over from the elimination of the aspects that used the axiom of step 2.
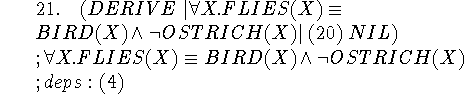
DERIVE straightens out 20 to put the conclusion in the desired form. The result is still dependent on the assumption of the correctness of the circumscription made in step 4.
Clearly if circumscription is to become a practical technique, the reasoning has to become much more automatic.