In order to keep the example short we will take into account only the following facts from the earlier section on flying.
Their conjunction is taken as A(ab,flies). This means
that what entities satisfy ab and what entities satisfy flies are
to be chosen so as to minimize 
. Which objects are birds
and ostriches are parameters rather than variables, i.e.
what objects are birds is considered given.
We also need an axiom that asserts that the aspects are different. Here is a straightforward version that would be rather long were there more than three aspects.
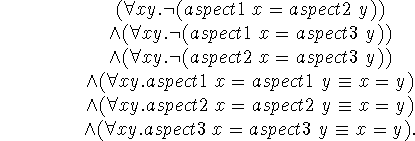
We could include this axiom in A(ab,flies), but as we shall see,
it won't matter whether we do, because it contains neither ab nor
flies.
The circumscription formula 
is then
A(ab,flies) is guaranteed to be true, because it is part of what is assumed in our common sense database. Therefore (42) reduces to
Our objective is now to make suitable substitutions for 
and
so that all the terms preceding the 
in
(43) will be true,
and the right side will determine ab. The axiom A(ab,flies) will then
determine flies, i.e. we will know what the fliers are.
is easy, because we need only apply wishful
thinking; we want the fliers to be just those birds that aren't ostriches.
Therefore, we put
isn't really much more difficult, but there is a notational
problem. We define
which covers the cases we want to be abnormal.
Appendix A contains a complete proof as accepted by Jussi Ketonen's (1984) interactive theorem prover EKL. EKL uses the theory of types and therefore has no problem with the second order logic required by circumscription.
