In ordinary mathematical language, there are certain tools for defining new functions in terms of old ones. These tools are composition and the identification of variables. As it happens, these tools are inadequate computable in terms of old ones. It is then customary to define all functions that can reasonably be regarded as to give a verbal definition. For example, the function |x| is usually defined in words.
If we add a single formal tool, namely conditional expressions to our mathematical notation, and if we allow conditional expressions to be used recursively in a manner that I shall describe, we can define, in a completely formal way, all functions that can reasonably be regarded as computable in terms of an initial set. We will use the ALGOL 60 notation for conditional expressions in this paper.
We shall use conditional expressions in the simple form
![]()
where p is a propositional expression whose value is true or false. The value of the conditional expression is a if p has the value true and b if p has the value false. When conditional expressions are used, the stock of predicates one has available for constructing p's is just as important as the stock of ordinary functions to be used in forming the a's and b's by composition. The following are examples of functions defined by conditional expressions:
The first of these is the only non-recursive definition
in the group. Next, we have three different procedures
for computing n!; they can be shown to be equivalent
by the methods to be described in this paper. Then we
define the predecessor function ![]() for positive integers
for positive integers
![]() in terms of the successor function
in terms of the successor function ![]() Finally, we define addition in terms of the successor,
the predecessor and equality. In all of the definitions,
except for the first, the domain of the variables is taken
to be the set of non-negative integers.
Finally, we define addition in terms of the successor,
the predecessor and equality. In all of the definitions,
except for the first, the domain of the variables is taken
to be the set of non-negative integers.
As an example of the use of these definitions, we shall show how to compute 2! by the second definition of n!. We have
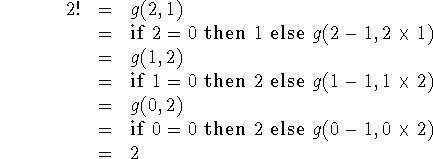
Note that if we attempted to compute n! for any n but a non-negative integer the successive reductions would not terminate. In such cases we say that the computation does not converge. Some recursive functions converge for all values of their arguments, some converge for some values of the arguments, and some never converge. Functions that always converge are called total functions, and the others are called partial functions. One of the earliest major results of recursive function theory is that there is no formalism that gives all the computable total functions and no partial functions.
We have proved [McC63] that the above method of defining
computable functions, starting from just the successor
function ![]() and equality, yields all the computable
functions of integers. This leads us to assert that we
have the complete set of tools for defining functions
which are computable in terms of given base functions.
and equality, yields all the computable
functions of integers. This leads us to assert that we
have the complete set of tools for defining functions
which are computable in terms of given base functions.
If we examine the next to last line of our computation of 2! we see that we cannot simply regard the conditional expression
![]()
as a function of the three quantities p, a, and b. If we did so, we would be obliged to compute g(-1, 0) before evaluating the conditional expression, and this computation would not converge. What must happen is that when p is true we take a as the value of the conditional expression without even looking at b.
Any reference to recursive functions in the rest of this paper refers to functions defined by the above methods.