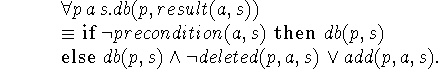
John McCarthy
Computer Science Department
Stanford University
Stanford, CA 94305
jmc@cs.stanford.edu
http://www-formal.stanford.edu/jmc/
JanFebMarAprMayJun
JulAugSepOctNovDec , :< 10 0
[This is a 1985 note with modernized typography.]
STRIPS [FN71] is a planning system that uses logical formulas to represent information about a state. Each action has a precondition, an add list and a delete list. When an action is considered, it is first determined whether its precondition is satisfied. This can be done by a theorem prover, but my understanding is that the preconditions actually used are simple enough that whether one is true doesn't require substantial theorem proving. If the precondition isn't met, then another action must be tried. If the precondition is met, then then sentences on the delete list are deleted from the database and sentences on the add list are added to it. STRIPS was considered to be an improvement on earlier systems [Gre69] using the situation calculus, because these earlier systems ran too slowly.
It was often said that STRIPS was just a specialization of the situation calculus that ran faster. However, it wasn't easy to see how to model a system with delete lists in the situation calculus. In this paper we present a situation calculus formalization of a version of STRIPS. Whether it is the full STRIPS isn't entirely clear. The reader will notice that a large amount of reification is done.
We have situations denoted by s sometimes with subscripts. The initial situation is often called s0. We also have proposition variables p and q sometimes with subscripts. Associated with each situation is a database of propositions, and this gives us the wff db(p,s) asserting that p is in the database associated with s. We action variables a, possibly subscripted, and have the function result, where s' = result(a,s) is the situation that results when action a is performed in situation s.
STRIPS is characterized by three predicates.
precondition(a,s) is true provided action a can be performed in situation s.
deleted(p,a,s) is true if proposition p is to be deleted when action a is performed in situation s.
add(p,a,s) is true if proposition p is to be added when action a is performed in situation s.
STRIPS has the single axiom
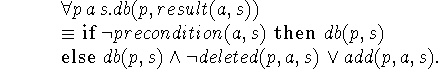
We now give an example of this use of STRIPS in the blocks world. Our individual variables x, y and z range over blocks. The constant blocks used in the example are a, b, c, d and Table. The one kind of proposition is on(x,y) asserting that block x is on block y. The one kind of action is move(x,y) denoting the act of moving block x on top of block y. We assume the blocks are all different, i.e.
We will be interested in an initial situation s0 characterized by
Next we characterize the predicates precondition, delete and add. We have
and
From these axioms and the initial conditions given above we can prove
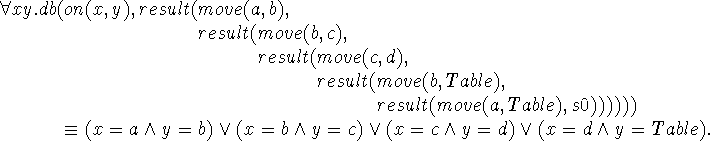
Remarks:
1. In order to handle deleting we made the database explicit and reified propositions. This allowed us to quantify over propositions.
2. Since the precondition was expressible conveniently in terms of the presence of sentences in the database, we didn't require a logic of propositions. Such a logic can be given by introducing an additional predicate holds(p,s) and the axiom
together with axioms like
and
We can then express preconditions in terms of what holds and not merely what is in the database. However, holds(p,s) will only be very powerful if the propositions can contain quantifiers. This raises some difficulties which we don't want to treat in this note but which are discussed in [McC79]. Keeping holds(p,s) conceptually separate from db(p,s) means that what holds is updated each time the situation changes.
3. The database in the blocks world example consists of independent atomic constant propositions. These can be added and deleted independently. For this reason there is no difficulty in determining what remains true when a proposition is deleted (or rather what propositions are true in result(a,s)).
4. Nilsson points out (conversation 1985 February 4) that we might want more complex propositions to persist rather than be recomputed. For example, we might have clear(x) defined by
and when move(w,z) occurs with 
and 
, we would like
to avoid recomputing 
. Obviously this can be done.
5. This formulation does no non-monotonic reasoning.
The use of 
enables us to completely characterize the set of
blocks in s0 and to preserve complete knowledge about the
situation resulting from moving blocks. The role of non-monotonic
reasoning in these simple situations needs to be studied. Compare
[McC86].
6. Because this formalism reifies propositions, there need
not be an identity between logical consistency and consistency of
the propositions in their intended meaning. For example,
holds(p,s) and 
are consistent unless we have
an axiom forbidding it, e.g. 
.
This axiom may be stronger than we want, because it may be convenient
to use an interpretation of holds in which neither holds(p,s)
nor holds(not p,s) is true.
7. As Vladimir Lifschitz [Lif87] has pointed out, a working STRIPS system may be unstable with regard to adding true propositions to the database, because unless the proposition is deleted when its truth value changes, it can lead to inconsistency when an action is performed. This instability is a defect of STRIPS and other systems in which updating is performed by other means than deduction.
8. As long as much of the knowledge is encoded in the updating rules, the information encoded in sentences may be minimal.
9. Many of the considerations discussed here concerning STRIPS apply to other semi-logical formalisms, e.g. EMYCIN and ART. [1997 note: They also apply to linear logic and Wolfgang Bibel's formalism TR.]