As was shown in Section 4, the condition for a room being stuffy is better formalized with effect axioms, occurrence axioms, and the events Getstuffy and Ungetstuffy. Lin and Reiter [LR94] consider the Emperor's decree that no more than one object (block) be yellow, which may be regarded as a domain constraint. They point out that it is more efficient to encode the constraint as a precondition that a block may be painted yellow only if no block is already yellow. Their way of expressing this does not readily elaborate to require that no more than seven blocks be yellow.
I think logical AI needs a more complex treatment. It seems to me that efficiency conflicts with generality. It is bad or dangerous to have more than one yellow block, but perhaps only if one is not a special favorite of the emperor or if one is just about to die anyway. The point is that common sense (at least human level common sense) requires that such constraints tolerate elaboration. Human level common sense also allows the constraint to become an action precondition as a result of some inference. This inference should take place within the logical formalization.
Lin and Reiter include the following formula.
This formula is specialized to the emperor tolerating just one yellow
block. If he tolerates 7 yellow blocks, we had better use set
notation, i.e. refer to 
.
There are some domain constraints that are not naturally formalized by internal actions. One is the blocks world constraint that a block may not be on top of itself. Formulas like
or even
tell more about the world than the simple
An important application for the direct use of state constraints is when an event starts a process that eventually leads to an equilibrium state. For example, if I drop a coin on the floor it will bounce around for a while and then settle down. It will reach equilibrium in a second or so, and I am interested in whether the coin ends up heads or tails rather than in the process of its settling down. In the case of the coin the equilibrium condition, at least what we want to know about it, is easy to state, namely
where using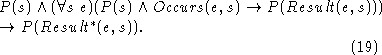 
means that we are skipping by some internal
events, in this case not formalized.
Another example may be concocted from the elaborated stuffy room scenario. While Pat and Mike disagree in their preferences, under normal circumstances we can suppose they will come to an agreement in some short time. One will defer to the other in the matter of the blocked vents. As with the coins, the theory of eventual agreement doesn't predict what the agreement will be.
More generally, Aarati Parmar suggests that internal events are evoked by any non-equilibrium situations.
