Since both the usual form of computer program and recursive function definitions are universal computationally, it is interesting to display the relation between them. The translation of recursive symbolic functions into computer programs was the subject of the rest of this report. In this section we show how to go the other way, at least in principle.
The state of the machine at any time during a computation
is given by the values of a number of variables. Let these variables be
combined into a vector ![]() . Consider a program block with one entrance
and one exit. It defines and is essentially defined by a certain
function
. Consider a program block with one entrance
and one exit. It defines and is essentially defined by a certain
function ![]() that takes one machine configuration into another, that is,
that takes one machine configuration into another, that is,
![]() has the form
has the form ![]() . Let us call
. Let us call ![]() the associated
function
of the
program block. Now let a number of such blocks be combined into a
program by decision elements
the associated
function
of the
program block. Now let a number of such blocks be combined into a
program by decision elements ![]() that decide after each block is
completed which block will be entered next. Nevertheless, let the
whole program still have one entrance and one exit.
that decide after each block is
completed which block will be entered next. Nevertheless, let the
whole program still have one entrance and one exit.
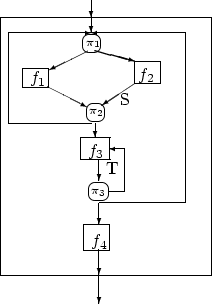
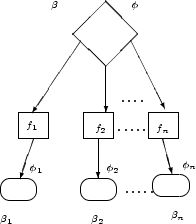
We give as an example the flowcart of figure 5. Let us
describe the function ![]() that gives the transformation of the vector
that gives the transformation of the vector
![]() between entrance and exit of the whole block. We shall define it in conjunction with the functions s(
between entrance and exit of the whole block. We shall define it in conjunction with the functions s(![]() ),
and t[
),
and t[![]() ], which give the transformations that
], which give the transformations that ![]() undergoes between
the points S and T, respectively, and the exit.
We have
undergoes between
the points S and T, respectively, and the exit.
We have
![\begin{eqnarray*}
r[\xi] &=& [\pi_11[\xi] \rightarrow S[f_1[\xi]]; T \rightarrow...
...]; \pi_32[\xi] \rightarrow r[\xi]; T \rightarrow t[f_3[\xi]]]\\
\end{eqnarray*}](img242.png)
Given a flowchart with a single entrance and a single exit, it is easy to write down the recursive function that gives the transformation of the state vector from entrance to exit in terms of the corresponding functions for the computation blocks and the predicates of the branch. In general, we proceed as follows.
In figure 6, let ![]() be an n-way branch point,
and let
be an n-way branch point,
and let
![]() be the computations leading to branch
points
be the computations leading to branch
points
![]() . Let
. Let ![]() be
the function that transforms
be
the function that transforms ![]() between
between ![]() and the exit of the
chart,
and let
and the exit of the
chart,
and let
![]() be the corresponding functions
for
be the corresponding functions
for
![]() . We then write
. We then write