

Next: The Customer as a
Up: Grouping supermarket purchases by
Previous: Grouping supermarket purchases by
One approach involves minimizing total anomaly in the assignment of
baskets to customers.
Definition: A partial assignment 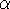 groups some
of the baskets of purchases according to whether they were purchased
by the same customer. Each group also includes an identifier c for the
customer and a classification class(c) of the customer. The
set of baskets associated with the putative customer c will be
denoted by baskets(c).
groups some
of the baskets of purchases according to whether they were purchased
by the same customer. Each group also includes an identifier c for the
customer and a classification class(c) of the customer. The
set of baskets associated with the putative customer c will be
denoted by baskets(c).
Definition: A complete assignment groups all of the
purchase baskets.
If there are N baskets in the database, there are something like
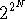 complete assignments--less because the customers may be
permuted.
complete assignments--less because the customers may be
permuted.
Definition: Associated with each assignment will be
a numerical total anomaly measuring how anomalous the assignment is.
The program's goal is to find an assignment (or maybe many
assignments) that minimize the total anomaly.
The total anomaly 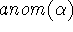 of an assignment
of an assignment 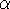 is the sum
of two main terms,
is the sum
of two main terms,
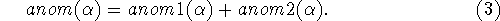
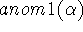 is itself a sum
is itself a sum
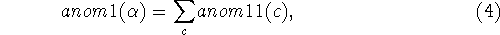
where the variable c ranges over the set of customers to which the
baskets are assigned. 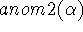 concerns global properties of
the set of assignments.
concerns global properties of
the set of assignments.
Definition: Associated with an assignment 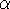 and a
customer c is a characterization
and a
customer c is a characterization 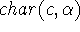 of the
putative customer. The characterization may include qualitative
characeristics like sex or owning a freezer, quantitative
characeristics like age or income group and other customer
characteristics like a certain purchase signature. The anomaly
anom11(c) associated with a customer c depends on the
characterization
of the
putative customer. The characterization may include qualitative
characeristics like sex or owning a freezer, quantitative
characeristics like age or income group and other customer
characteristics like a certain purchase signature. The anomaly
anom11(c) associated with a customer c depends on the
characterization 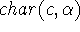 . Thus buying chewing tobacco or
baby food is more anomalous for some customers than others. A program
that generates assignments will generate characterizations as it
groups the baskets by customer. The characterization itself will
contribute to the anomaly if it is an unusual characterization.
. Thus buying chewing tobacco or
baby food is more anomalous for some customers than others. A program
that generates assignments will generate characterizations as it
groups the baskets by customer. The characterization itself will
contribute to the anomaly if it is an unusual characterization.
Definition: A signature is a set of choices among
alternate brands or sizes of certain commodities. The commodities
most useful for signatures are those for which variety is not
normally considered desirable. While a person may want variety in
food he is unlikely to want variety per se in dish-washing soap, toilet
paper or size of dog food. Signatures are included in the
characterization of a customer.
The part of the anomaly anom11(c) associated with the putative
customer c is computed relative to the characterization. Thus if
c is characterized as single young female, a purchase of chewing
tobacco should have a higher anomaly score than for a male.
One way of looking at minimizing anomaly of assignments is that we
want to explain as much of the purchasing behavior as possible by
allowable characterizations of the customers.
We regard the notions of minimizing anomaly in the space of
assignments as a guiding theoretical idea. Programs may find
complete assignments, but they are unlikely to do it by comparing a
large number of alternative complete assignments. Instead they are
likely to do hill climbing in the space of partial assignments.
Here are some kinds of terms that may be associated with the customer
part of the anomaly function.
- A measure of the temporal irregularity of the customer's
purchases. Perishable, non-freezable items like milk need to be
purchased at a fairly regular rate. If baby food is purchased, it
also is consumed at a regular rate, although it can be stored. Some
customers will be very irregular, but an assignment shouldn't make
most of them irregular.
- A measure of the extent to which the grouped baskets do not fit
the characterization
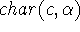 .
. - Signatures involving a large variation in brands of certain
items should contribute to the anomaly.
- A lot of variation in a putative customer's purchase quantity of a
frequently bought item. This suggests that the same person didn't
buy all those baskets.
- A customer buys food, stores it for a while and eats it.
Thus the contents his larder is a function of time. The database
tells about the purchasing but not directly about the eating or the
state of the larder. We can attribute a
larder function of time to
a customer as part of the ascription and use some measure of its
irregularity as a component of the anomaly.
Here are some ideas about programs for finding assignments.
- We hill climb in the space of partial assignments. For
example, moving a purchase from one customer to another may
reduce the anomaly of both customers' ascribed larder functions.
- We might proceed chronologically, assigning each basket to
either a previously postulated customer or to a new one.
- At first new customers would predominate. However, when the
number of postulated customers begins to get too large for the
number of baskets, the program would try to reduce the number by
combining baskets.
How can it be inferred that several cash purchases involved the same
customer? We only need to be correct often enough so that the
statistics come out right. Each customer has his own pattern of
purchases. Here are some considerations.
- The signature
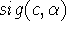 is a purchase pattern
unique to the customer c. Consider items where variety is not
normally desired, e.g. dishwasher soap. There are several brands, but
a customer will normally stick with one for quite a long time. If
there are 5 brands and 50 such kinds of items, there are enough
possible signatures to distinguish far more customers than a store
or even a chain is likely to have. Of course, a customer is
unlikely to purchase a complete signature package each time he goes
to the store, so partial signatures will have to be used.
is a purchase pattern
unique to the customer c. Consider items where variety is not
normally desired, e.g. dishwasher soap. There are several brands, but
a customer will normally stick with one for quite a long time. If
there are 5 brands and 50 such kinds of items, there are enough
possible signatures to distinguish far more customers than a store
or even a chain is likely to have. Of course, a customer is
unlikely to purchase a complete signature package each time he goes
to the store, so partial signatures will have to be used. - The ingredients for particular recipes are sometimes diagnostic,
especially when the recipe is unique to the customer or is a
standard recipe varied in a unique way.
- An important intermediate variable for a customer is the state
of his larder at a given time. He likes to have certain items in
stock in his refrigerator or freezer.
- The customer makes choices in a certain pattern, e.g. buys
creamy rather than chunky peanut butter. Which choices are made is
more indicative than whether peanut butter is bought at all on a
particular occasion, since the customer may not have run out yet.
- Suppose a store has 10,000 items and has 12,000 customers.
Suppose purchases average 20 items. My information theory intuition
suggests that there is enough information to identify the customers
over some 20 shopping trips. The information theory numbers can be
analyzed, but experiment is still required to determine feasibility.
- Sometimes it will be impossible to assign a basket to a
customer. As an extreme example, suppose that withing ten minutes
two customers each buy a six pack of the same brand of beer and
nothing else. Which one made which purchase will be impossible to
tell, but it won't matter which purchase is assigned to which
customer.


Next: The Customer as a
Up: Grouping supermarket purchases by
Previous: Grouping supermarket purchases by
John McCarthy
Wed Feb 23 17:08:25 PST 2000
![]() groups some
of the baskets of purchases according to whether they were purchased
by the same customer. Each group also includes an identifier c for the
customer and a classification class(c) of the customer. The
set of baskets associated with the putative customer c will be
denoted by baskets(c).
groups some
of the baskets of purchases according to whether they were purchased
by the same customer. Each group also includes an identifier c for the
customer and a classification class(c) of the customer. The
set of baskets associated with the putative customer c will be
denoted by baskets(c).
![]() complete assignments--less because the customers may be
permuted.
complete assignments--less because the customers may be
permuted.
![]() of an assignment
of an assignment ![]() is the sum
of two main terms,
is the sum
of two main terms,
![]()
![]() is itself a sum
is itself a sum
![]()
![]() concerns global properties of
the set of assignments.
concerns global properties of
the set of assignments.
![]() and a
customer c is a characterization
and a
customer c is a characterization ![]() of the
putative customer. The characterization may include qualitative
characeristics like sex or owning a freezer, quantitative
characeristics like age or income group and other customer
characteristics like a certain purchase signature. The anomaly
anom11(c) associated with a customer c depends on the
characterization
of the
putative customer. The characterization may include qualitative
characeristics like sex or owning a freezer, quantitative
characeristics like age or income group and other customer
characteristics like a certain purchase signature. The anomaly
anom11(c) associated with a customer c depends on the
characterization ![]() . Thus buying chewing tobacco or
baby food is more anomalous for some customers than others. A program
that generates assignments will generate characterizations as it
groups the baskets by customer. The characterization itself will
contribute to the anomaly if it is an unusual characterization.
. Thus buying chewing tobacco or
baby food is more anomalous for some customers than others. A program
that generates assignments will generate characterizations as it
groups the baskets by customer. The characterization itself will
contribute to the anomaly if it is an unusual characterization.