Our blocks world has 4 sorts, situations s, blocks b, locations l and actions a. These are all disjoint.
We have a situation constant S0, other situation constant Sn and
Sn' for various n's, a set of block constants 
, where 
and one block location constant
Table. We also have constants 
, 
and 
.
All blocks are unique, but we do not postulate domain closure.
We have block locations
, which are the Top of a block, or are the
Table.
All distinct block location terms denote distinct locations.
We have a function from actions and situations to situations,
, and a function from blocks and locations to actions,
, which gives the action where block b is moved to
location l.
All distinct action terms are distinct.
We have the foundational axioms for situation calculus we considered earlier.
We have fluents, 
which states that b is on location l
in situation s, and 
. is fully defined in terms of On.
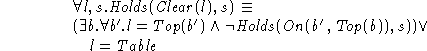
We now add the obvious definition of Changes for Move(b,l)
actions. That is, there is a change in On(b,l') and On(b,l) when
contains On(b,l') for an l' not equal to l, and 
, and 
contains Clear(l) and Clear(top(b)).
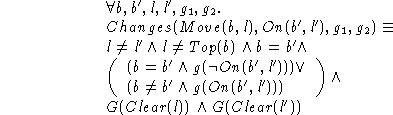
This concludes the axiomatization of blocksworld, we could add domain constraints, but this is not necessary for the reasoning we do in this paper. We now present an axiomatization of traveling, followed by an axiomatization of buying selling and sending and receiving.