This section is informal, because we want to discuss what the
consequences of a narrative should be before discussing how
to make circumscription or some other nonmonotonic formalism
do what we want. Here are some kinds of inference we want
to be able to make.
- Preconditions
- An action has only those preconditions that
can be inferred from the facts at hand.
- Ramifications
- Only the effects of an event that can be
inferred from the narrative are relevant to the future course of
the events mentioned in the narrative.
- Presence of objects
- The only objects satisfying certain
fluents in a situation are those for which it follows from what is
stated. Some of the ``it follows'' assertions are inferred
nonmonotonically. One child will infer that another child
has parents but not that the child has a dog.
- Normal effect
- An event has its normal effect unless
something prevents it.
- Occurrences
- Only such events occur in a situation or its
successors as are asserted or inferred or which don't affect
conclusions that might be drawn from their nonoccurrence.
This condition must be formalized very carefully, as is apparent
when we elaborate a particular event as a sequence of smaller
events. ``How did he buy the Kleenex? He took it off the shelf,
put it on the counter, paid the clerk and took it home.'' A
narrative that just mentions buying the Kleenex should not allow
nonmonotonic reasoning that excludes this particular elaboration.
Moreover, if we elaborate in this way, we don't want to exclude
subsequent elaboration of component events, e.g. elaborating
paying the clerk into offering a bill, taking the change, etc.
- Inertia
- Events change only those fluents they can
be inferred to change. Fluents or fluent valued functions
may be declared to be dependent by statements like
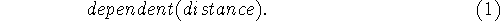
This statement would have the effect of making

change with changes in x and y and have no inertia
of its own.
Processes that have started in a situation continue until
something changes their course or they terminate as called
for in their axiomatizations.
- Obstacles
- Only such obstacles arise to events having their
normal effects as can be inferred.
- Actions
- Minimize unmotivated actions.
We will very likely use something like the Reiter and
Levesque technique of a two stage minimization. (Reiter's
Research Excellence lecture and subsequent discussions.)
(Advice to use this technique may serve as an example of
the declarative expression of heuristics.)
![]()