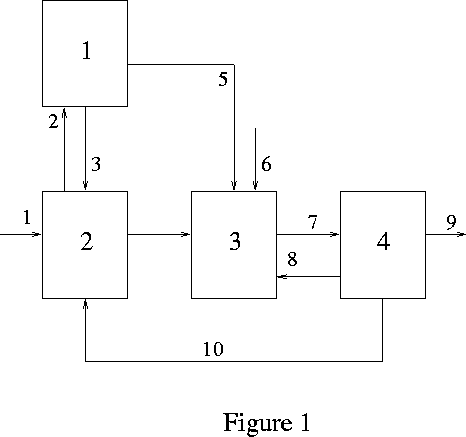
Let S be a system of interacting discrete finite automata such as that shown in Figure 1.
Each box represents a subautomaton and each line represents a signal. Time takes on integer values and the dynamic behaviour of the whole automaton is given by the equations:
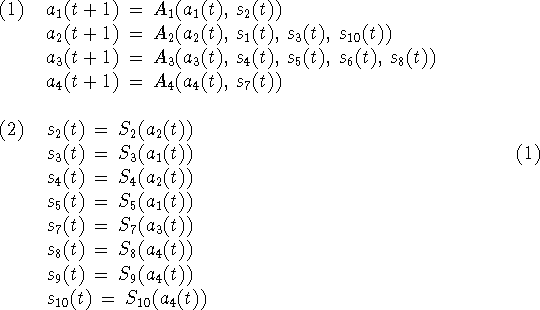
The interpretation of these equations is that the state of any automaton at time t+1 is determined by its state at time t and by the signals received at time t. The value of a particular signal at time t is determined by the state at time t of the automaton from which it comes. Signals without a source automaton represent inputs from the outside and signals without a destination represent outputs.
Finite automata are the simplest examples of systems that interact over time. They are completely deterministic; if we know the initial states of all the automata and if we know the inputs as a function of time, the behaviour of the system is completely determined by equations (1) and (2) for all future time.
The automaton representation consists in regarding the world as a system of interacting subautomata. For example, we might regard each person in the room as a subautomaton and the environment as consisting of one or more additional subautomata. As we shall see, this representation has many of the qualitative properties of interactions among things and persons. However, if we take the representation too seriously and attempt to represent particular situations by systems of interacting automata, we encounter the following difficulties:
1. The number of states required in the subautomata is very
large, for example 
, if we try to represent
someone's knowledge. Automata this large have to be
represented by computer programs, or in some other way
that does not involve mentioning states individually.
2. Geometric information is hard to represent. Consider, for example, the location of a multi-jointed object such as a person or a matter of even more difficulty--the shape of a lump of clay.
3. The system of fixed interconnections is inadequate. Since a person may handle any object in the room, an adequate automaton representation would require signal lines connecting him with every object.
4. The most serious objection, however, is that (in our terminology) the automaton representation is epistemologically inadequate. Namely, we do not ever know a person well enough to list his internal states. The kind of information we do have about him needs to be expressed in some other way.
Nevertheless, we may use the automaton representation for concepts of can, causes, some kinds of counterfactual statements (`If I had struck this match yesterday it would have lit') and, with some elaboration of the representation, for a concept of believes.
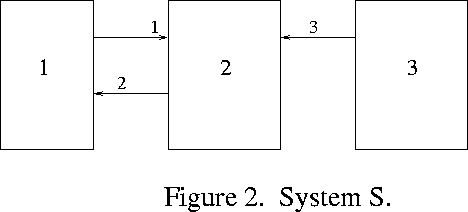
Let us consider the notion of can. Let S be a system of
subautomata without external inputs such as that of Figure 2. Let
p be one of the subautomata, and suppose that there are m signal
lines coming out of p. What p can do is defined in terms of a
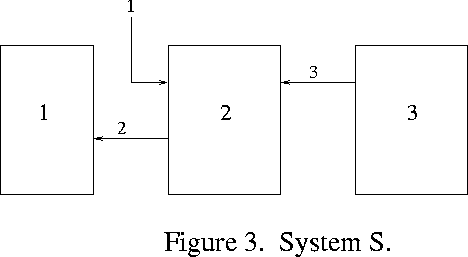
new system 
, which is obtained from the system S by
disconnecting the m signal lines coming from p and replacing them
by m external input lines to the system. In Figure 2, subautomaton
1 has one output, and in the system 
(Figure 3) this is replaced by an
external input. The new system always has the same set of
states as the system S. Now let 
be a condition on the state
such as, ` 
is even' or ` 
'. (In the applications may
be a condition like `The box is under the bananas'.)
We shall write
which is read, `The subautomaton p can bring about the condition
in the situation s' if there is a sequence of outputs from the
automaton that will eventually put S into a state a' that
satisfies 
. In other words, in determining what p can
achieve, we consider the effects of sequences of its actions, quite
apart from the conditions that determine what it actually will do.
In Figure 2, let us consider the initial state a to be one in which all subautomata are initially in state 0. Then the reader will easily verify the following propositions:
1. Subautomaton 2 will never be in state 1.
2. Subautomaton 1 can put subautomaton 2 in state 1.
3. Subautomaton 3 cannot put subautomaton 2 in state 1.
We claim that this notion of can is, to a first approximation, the appropriate one for an automaton to use internally in deciding what to do by reasoning. We also claim that it corresponds in many cases to the common sense notion of can used in everyday speech.
In the first place, suppose we have an automaton that decides what to do by reasoning; for example, suppose it is a computer using an RP. Then its output is determined by the decisions it makes in the reasoning process. It does not know (has not computed) in advance what it will do, and, therefore, it is appropriate that it considers that it can do anything that can be achieved by some sequence of its outputs. Common-sense reasoning seems to operate in the same way.
The above rather simple notion of can requires some
elaboration, both to represent adequately the commonsense notion and
for practical purposes in the reasoning program.
First, suppose that the system of automata admits external
inputs. There are two ways of defining can in this case. One way
is to assert 
if p can achieve regardless of what
signals appear on the external inputs. Thus, we require
the existence of a sequence of outputs of p that achieves the goal
regardless of the sequence of external inputs to
the system. Note that, in this definition of can, we are
not requiring that p have any way of knowing what the external
inputs were. An alternative definition requires the outputs to
depend on the inputs of p. This is equivalent to saying that p
can achieve a goal, provided the goal would be achieved for arbitrary
inputs by some automaton put in place of p. With either of these
definitions can becomes a function of the place of the subautomaton
in the system rather than of the subautomaton itself. We do not know
which of these treatments is preferable, and so we shall call the
first concept cana and the second canb.
The idea that what a person can do depends on his position rather than on his characteristics is somewhat counter-intuitive. This impression can be mitigated as follows: Imagine the person to be made up of several subautomata; the output of the outer subautomaton is the motion of the joints. If we break the connection to the world at that point we can answer questions like, `Can he fit through a given hole?' We shall get some counter-intuitive answers, however, such as that he can run at top speed for an hour or can jump over a building, since these are sequences of motions of his joints that would achieve these results.
The next step, however, is to consider a subautomaton that receives the nerve impulses from the spinal cord and transmits them to the muscles. If we break at the input to this automaton, we shall no longer say that he can jump over a building or run long at top speed since the limitations of the muscles will be taken into account. We shall, however, say that he can ride a unicycle since appropriate nerve signals would achieve this result.
The notion of can corresponding to the intuitive notion in the largest number of cases might be obtained by hypothesizing an organ of will, which makes decisions to do things and transmits these decisions to the main part of the brain that tries to carry them out and contains all the knowledge of particular facts. If we make the break at this point we shall be able to say that so-and-so cannot dial the President's secret and private telephone number because he does not know it, even though if the question were asked could he dial that particular number, the answer would be yes. However, even this break would not give the statement, `I cannot go without saying goodbye, because this would hurt the child's feelings'.
On the basis of these examples, one might try to postulate a sequence of narrower and narrower notions of can terminating in a notion according to which a person can do only what he actually does. This notion would then be superfluous. Actually, one should not look for a single best notion of can; each of the above-mentioned notions is useful and is actually used in some circumstances. Sometimes, more than one notion is used in a single sentence, when two different levels of constraint are mentioned.
Besides its use in explicating the notion of can, the
automaton representation of the world is very suited for defining
notions of causality. For, we may say that subautomaton p caused
the condition in state s, if changing the output of p would
prevent . In fact the whole idea of a system of interacting
automata is just a formalization of the commonsense notion of
causality.
Moreover, the automaton representation can be used to
explicate certain counterfactual conditional sentences. For example,
we have the sentence, `If I had struck this match yesterday at this
time it would have lit.' In a suitable automaton representation, we
have a certain state of the system yesterday at that time, and we
imagine a break made where the nerves lead from my head or perhaps at
the output of my `decision box', and the appropriate signals to
strike the match having been made. Then it is a definite and
decidable question about the system 
, whether the match lights
or not, depending on whether it is wet, etc. This interpretation of
this kind of counterfactual sentence seems to be what is needed for
RP to learn from its mistakes, by accepting or generating sentences
of the form, `had I done thus-and-so I would have been successful, so
I should alter my procedures in some way that would have produced the
correct action in that case'.
In the foregoing we have taken the representation of the situation as a system of interacting subautomata for granted. However, a given overall situation might be represented as a system of interacting subautomata in a number of ways, and different representations might yield different results about what a given subautomaton can achieve, what would have happened if some subautomaton had acted differently, or what caused what. Indeed, in a different representation, the same or corresponding subautomata might not be identifiable. Therefore, these notions depend on the representation chosen.
For example, suppose a pair of Martians observe the situation in a room. One Martian analyzes it as a collection of interacting people as we do, but the second Martian groups all the heads together into one subautomaton and all the bodies into another. (A creature from momentum space would regard the Fourier components of the distribution of matter as the separate interacting subautomata.) How is the first Martian to convince the second that his representation is to be preferred? Roughly speaking, he would argue that the interaction between the heads and bodies of the same person is closer than the interaction between the different heads, and so more of an analysis has been achieved from `the primordial muddle' with the conventional representation. He will be especially convincing when he points out that when the meeting is over the heads will stop interacting with each other, but will continue to interact with their respective bodies.
We can express this kind of argument formally in terms of
automata as follows: Suppose we have an autonomous automaton A,
that is an automaton without inputs, and let it have k states.
Further, let m and n be two integers such that 
. Now
label k points of an m-by-n array with the states of A. This
can be done in 
ways. For each of these ways we have a
representation of the automaton A as a system of an m-state
automaton B interacting with an n-state automaton C. Namely,
corresponding to each row of the array we have a state of B and to
each column a state of C. The signals are in 1-1 correspondence
with the states themselves; thus each subautomaton has just as many
values of its output as it has states. Now it may happen that two of
these signals are equivalent in their effect on the other
subautomaton, and we use this equivalence relation to form
equivalence classes of signals. We may then regard the equivalence
classes as the signals themselves. Suppose then that there are now
r signals from B to C and s signals from C to B. We ask
how small r and s can be taken in general compared to m and
n. The answer may be obtained by counting the number of
inequivalent automata with k states and comparing it with the
number of systems of two automata with m and n states
respectively and r and s signals going in the respective
directions. The result is not worth working out in detail, but tells
us that only a few of the k state automata admit such a
decomposition with r and s small compared to m and n.
Therefore, if an automaton happens to admit such a decomposition it
is very unusual for it to admit a second such decomposition that is
not equivalent to the first with respect to some renaming of states.
Applying this argument to the real world, we may say that it is
overwhelmingly probable that our customary decomposition of the world
automaton into separate people and things has a unique, objective and
usually preferred status. Therefore, the notions of can, of
causality, and of counterfactual associated with this decomposition
also have a preferred status.
In our opinion, this explains some of the difficulty philosophers have had in analyzing counterfactuals and causality. For example, the sentence, `If I had struck this match yesterday, it would have lit' is meaningful only in terms of a rather complicated model of the world, which, however, has an objective preferred status. However, the preferred status of this model depends on its correspondence with a large number of facts. For this reason, it is probably not fruitful to treat an individual counterfactual conditional sentence in isolation.
It is also possible to treat notions of belief and knowledge
in terms of the automaton representation. We have not worked this
out very far, and the ideas presented here should be regarded as
tentative. We would like to be able to give conditions under which
we may say that a subautomaton p believes a certain proposition.
We shall not try to do this directly but only relative to a predicate
. Here s is the state of the automaton p and w is
a proposition; is true if p is to be regarded as
believing w when in state s and is false otherwise. With respect
to such a predicate B we may ask the following questions:
1. Are p's beliefs consistent? Are they correct?
2. Does p reason? That is, do new beliefs arise that are logical consequences of previous beliefs?
3. Does p observe? That is, do true propositions about automata connected to p cause p to believe them?
4. Does p behave rationally? That is, when p believes a sentence asserting that it should do something does p do it?
5. Does p communicate in language L? That is, regarding the content of a certain input or output signal line as in a text in language L, does this line transmit beliefs to or from p?
6. Is p self-conscious? That is, does it have a fair variety of correct beliefs about its own beliefs and the processes that change them?
It is only with respect to the predicate 
that all these
questions can be asked. However, if questions 1 thru 4 are answered
affirmatively for some predicate , this is certainly
remarkable, and we would feel fully entitled to consider a
reasonable notion of belief.
In one important respect the situation with regard to belief
or knowledge is the same as it was for counterfactual conditional
statements: no way is provided to assign a meaning to a single
statement of belief or knowledge, since for any single statement a
suitable can easily be constructed. Individual statements
about belief or knowledge are made on the basis of a larger system
which must be validated as a whole.