Actions can be combined into strategies. The simplest combination is a finite sequence of actions. We shall combine actions as though they were ALGOL statements, that is, procedure calls. Thus, the sequence of actions, (`move the box under the bananas', `climb onto the box', and `reach for the bananas') may be written:
A strategy in general will be an ALGOL-like compound statement containing actions written in the form of procedure calling assignment statements, and conditional go to's. We shall not include any declarations in the program since they can be included in the much larger collection of declarative sentences that determine the effect of the strategy.
Consider for example the strategy that consists of walking 17 blocks south, turning right and then walking till you come to Chestnut Street. This strategy may be written as follows:
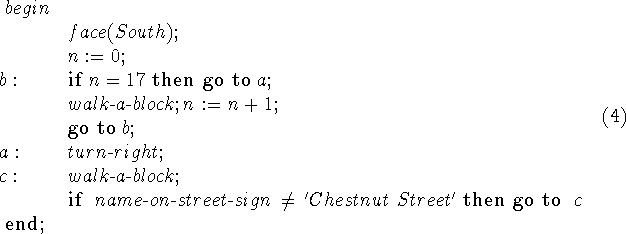
In the above program the external actions are represented by procedure calls. Variables to which values are assigned have a purely internal significance (we may even call it mental significance) and so do the statement labels and the go to statements.
For the purpose of applying the mathematical theory of
computation we shall write the program differently: namely, each
occurrence of an action 
is to be replaced by an assignment
statement 
Thus the above program becomes
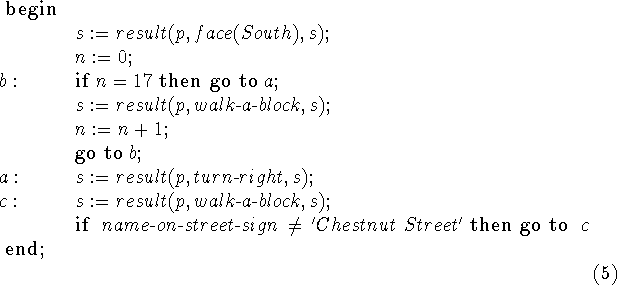
Suppose we wish to show that by carrying out this strategy John can
go home provided he is initially at his office. Then according to
the methods of Zohar Manna (1968a, 1968b), we may derive from this
program together with the initial condition 
and the final condition at(John,home(John),s), a
sentence W of first-order logic. Proving W will show that the
procedure terminates in a finite number of steps and that when it
terminates s will satisfy at(John, home(John),s).
According to Manna's theory we must prove the following collection of sentences inconsistent for arbitrary interpretations of the predicates q1 and q2 and the particular interpretations of the other functions and predicates in the program:
Therefore the formula that has to be proved may be written
In order to prove this sentence we would have to use the following kinds of facts expressed as sentences or sentence schemas of first-order logic:
1. Facts of geography. The initial street stretches at least 17 blocks to the south, and intersects a street which in turn intersects Chestnut Street a number of blocks to the right; the location of John's home and office.
2. The fact that the fluent 
will have
the value `Chestnut Street' at that point.
3. Facts giving the effects of action expressed as
predicates about 
deducible from sentences
about s.
4. An axiom schema of induction that allows us to deduce that the loop of walking 17 blocks will terminate.
5. A fact that says that Chestnut Street is a finite number of blocks to the right after going 17 blocks south. This fact has nothing to do with the possibility of walking. It may also have to be expressed as a sentence schema or even as a sentence of second-order logic.
When we consider making a computer carry out the strategy, we must
distinguish the variable s from the other variables in the second
form of the program. The other variables are stored in the memory of
the computer and the assignments may be executed in the normal way.
The variable s represents the state of the world and the computer
makes an assignment to it by performing an action. Likewise the
fluent requires an action, of observation.