It seemed to me in 1958 that small modifications in behavior are most often representable as small modifications in beliefs about the world, and this requires a system that represents beliefs explicitly.
``If one wants a machine to be able to discover an abstraction, it seems most likely that the machine must be able to represent this abstraction in some relatively simple way'' (McCarthy 1959).
The 1958 idea for increasing generality was to use logic to express facts in a way independent of the way the facts might subsequently be used. It seemed then and still seems that humans communicate mainly in declarative sentences rather than in programming languages for good objective reasons that will apply whether the communicator is a human, a creature from Alpha Centauri or a computer program. Moreover, the advantages of declarative information also apply to internal representation. The advantage of declarative information is one of generality. The fact that when two objects collide they make a noise may be used in particular situations to make a noise, to avoid making noise, to explain a noise or to explain the absence of noise. (I guess those cars didn't collide, because while I heard the squeal of brakes, I didn't hear a crash).
Once one decides to build an AI system that represents
information declaratively, one still has to decide what kind of
declarative language to allow. The simplest systems allow only
constant predicates applied to constant symbols, e.g.
on(Block1,Block2). Next one can allow arbitrary constant terms,
built from function symbols, constants and predicate symbols, e.g.
location(Block1) = top(Block2). Prolog databases
allow arbitrary Horn clauses that include free variables, e.g.
, expressing the Prolog in standard
logical notation. Beyond that lies full first order logic
including both existential and universal quantifiers and
arbitrary first order formulas. Within first order logic,
the expressive power of a theory depends on what domains the
variables are allowed to range. Important expressive power
comes from using set theory which contains expressions for
sets of any objects in the theory.
Every increase in expressive power carries a price in the required complexity of the reasoning and problem solving programs. To put it another way, accepting limitations on the expressiveness of one's declarative information allows simplification of the search procedures. Prolog represents a local optimum in this continuum, because Horn clauses are medium expressive but can be interpreted directly by a logical problem solver.
One major limitation that is usually accepted is to limit the derivation of new facts to formulas without variables, i.e to substitute constants for variables and then do propositional reasoning. It appears that most human daily activity involves only such reasoning. In principle, Prolog goes slightly beyond this, because the expressions found as values of variables by Prolog programs can themselves involve free variables. However, this facility is rarely used except for intermediate results.
What can't be done without more of predicate calculus than Prolog allows is universal generalization. Consider the rationale of canning. We say that a container is sterile if it is sealed and all the bacteria in it are dead. This can be expressed as a fragment of a Prolog program as follows.
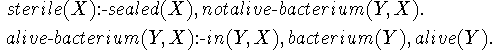
However, a Prolog program incorporating this fragment directly can sterilize a container only by killing each bacterium individually and would require that some other part of the program successively generate the names of the bacteria. It cannot be used to discover or rationalize canning -- sealing the container and then heating it to kill all the bacteria at once. The reasoning rationalizing canning involves the use of quantifiers in an essential way.
My own opinion is that reasoning and problem solving programs will eventually have to allow the full use of quantifiers and sets and have strong enough control methods to use them without combinatorial explosion.
While the 1958 idea was well received, very few attempts were made to embody it in programs in the immediately following years, the main one being F. Black's Harvard PhD thesis of 1964. I spent most of my time on what I regarded as preliminary projects, mainly LISP. My main reason for not attempting an implementation was that I wanted to learn how to express common sense knowledge in logic first. This is still my goal. I might be discouraged from continuing to pursue it if people pursuing nonlogical approaches were having significant success in achieving generality.
(McCarthy and Hayes 1969) made the distinction between epistemological and heuristic aspects of the AI problem and asserted that generality is more easily studied epistemologically. The distinction is that the epistemology is completed when the facts available have as a consequence that a certain strategy is appropriate to achieve the goal, while the heuristic problem involves the search that finds the appropriate strategy.
Implicit in (McCarthy 1959) was the idea of a general purpose common sense database. The common sense information possessed by humans would be written as logical sentences and included in the database. Any goal-seeking program could consult the database for the facts needed to decide how to achieve its goal. Especially prominent in the database would be facts about the effects of actions. The much studied example is the set of facts about the effects of a robot trying to move objects from one location to another. This led in the 1960s to the situation calculus (McCarthy and Hayes 1969) which was intended to provide a way of expressing the consequences of actions independent of the problem.
The basic formalism of the situation calculus is
which asserts that s' is the situation that results when event e occurs in situation s. Here are some situation calculus axioms for moving and painting blocks.
=0pt Qualified Result-of-Action Axioms
Frame Axioms
Notice that all qualifications to the performance of the actions are explicit in the premisses and that statements (called frame axioms) about what doesn't change when an action is performed are explicitly included. Without those statements it wouldn't be possible to infer much about result(e2,result(e1,s)), since we wouldn't know whether the premisses for the event e2 to have its expected result were fulfilled in result(e1,s).
Futhermore, it should be noticed that the situation calculus applies only when it is reasonable to reason about discrete events, each of which results in a new total situation. Continuous events and concurrent events are not covered.
Unfortunately, it wasn't very feasible to use the situation calculus in the manner proposed, even for problems meeting its restrictions. In the first place, using general purpose theorem provers made the programs run too slowly, since the theorem provers of 1969 (Green 1969) had no way of controlling the search. This led to STRIPS (Fikes and Nilsson 1971) which reduced the use of logic to reasoning within a situation. Unfortunately, the STRIPS formalizations were much more special than full situation calculus. The facts that were included in the axioms had to be delicately chosen in order to avoid the introduction of contradictions arising from the failure to delete a sentence that wouldn't be true in the situation that resulted from an action.