This section treats Poss(P,s) for finite automata. Finite automata raise the question of what an agent can do in a sharp form. However, they are not a useful representation of an agent's introspective knowledge of what it can do.
To the extent that a person or machine can achieve any of different goals, that person or machine has free will. Our ideas on this show up most sharply considering systems of interacting discrete finite automata. These are as deterministic as you can get, which is why I chose them to illustrate free will.
The material of this section is a revision of that in [McCarthy and Hayes 1969], section 2.4 entitled ``The automaton representation and the notion of can''.
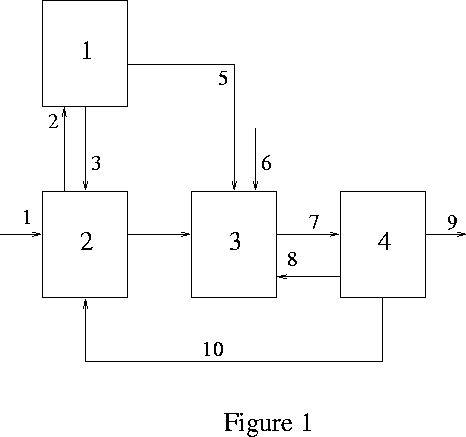
Let S be a system of interacting discrete finite automata such as that shown in Figure 1.
Each box represents a subautomaton and each line represents a signal. Time takes on integer values and the dynamic behavior of the whole automaton is given by the equations:
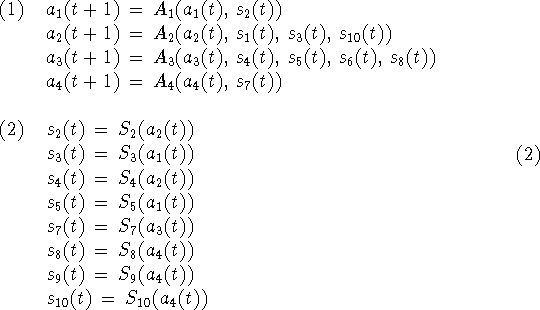
The interpretation of these equations is that the state of any subautomaton at time t+1 is determined by its state at time t and by the signals received at time t. The value of a particular signal at time t is determined by the state at time t of the automaton from which it comes. Signals without a source subautomaton represent inputs from the outside and signals without a destination represent outputs.
Finite automata are the simplest examples of systems that interact over time. They are completely deterministic; if we know the initial states of all the automata and if we know the inputs as a function of time, the behavior of the system is completely determined by equations (1) and (2) for all future time.
The automaton representation consists in regarding the world as a system of interacting subautomata. For example, we might regard each person in the room as a subautomaton and the environment as consisting of one or more additional subautomata. As we shall see, this representation has many of the qualitative properties of interactions among things and persons. However, if we take the representation too seriously and attempt to represent particular interesting systems as systems of interacting automata, we encounter the following difficulties:
1. The number of states required in the subautomata is very large, for
example 
, if we try to represent a person's knowledge.
Automata this large have to be represented by systems of equations or
by computer programs, or in some other way that does not involve
mentioning states individually. In Section 4 we'll
represent them partially, by sentences of logic.
2. Geometric information is hard to represent. Consider, for example, the location of a multi-jointed object such as a person or a matter of even more difficulty--the shape of a lump of clay.
3. The system of fixed interconnections is inadequate. Since a person may handle any object in the room, an adequate automaton representation would require signal lines connecting him with every object.
4. The most serious objection, however, is that (in the terminology of [McCarthy and Hayes 1969]) the automaton representation is epistemologically inadequate. Namely, we do not ever know a person well enough to list his internal states. The kind of information we do have about him needs to be expressed in some other way.
Nevertheless, we may use the automaton representation for concepts of can, causes, useful kinds of counterfactual statements (`If another car had come over the hill when you passed just now, there would have been a head-on collision'). See [Costello and McCarthy 1999].
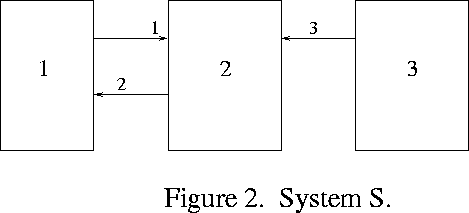
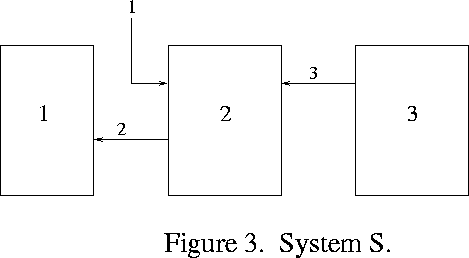
Let us consider the notion of can. Let S be a system of
subautomata without external inputs such as that of Figure 2. Let
p be one of the subautomata, and suppose that there are m signal
lines coming out of p. What p can do is defined in terms of a
new system 
, which is obtained from the system S by
disconnecting the m signal lines coming from p and replacing them
by m external input lines to the system. In Figure 2, subautomaton
1 has one output, and in the system 
(Figure 3) this is replaced by an
external input. The new system always has the same set of
states as the system S. Now let 
be a condition on the state
such as, ` 
is even' or ` 
'. (In the applications may
be a condition like `The box is under the bananas'.)
We shall write
which is read, `The subautomaton p can bring about the condition
in the situation s' if there is a sequence of outputs from the
automaton that will eventually put S into a state a' that
satisfies 
. In other words, in determining what p can
achieve, we consider the effects of sequences of its actions, quite
apart from the conditions that determine what it actually will do.
Here's an example based on Figure 2. In order to write formulas conveniently, we use natural numberss for the values of the states of the subautomata and the signals.
Consider the initial state of S to be one in which all the subautomata are in state 0. We have the following propositions:
1. Subautomaton 2 will never be in state 1. [It starts in state 0 and goes to state 2 at time 1. After that it can never decrease.]
2. Subautomaton 1 can put Subautomaton 2 in state 1 but won't. [If Subautomaton 1 emitted 1 at time 0 instead of 2, Subautomaton 2 would go to state 1.]
3. Subautomaton 3 cannot put Subautomaton 2 in state 1. [The output from Subautomaton 1 suffices to put Subautomaton 2 in state 1 at time 1, after which it can never decrease.]
We claim that this notion of can is, to a first approximation, the appropriate one for a robot to use internally in deciding what to do by reasoning. We also claim that it corresponds in many cases to the common sense notion of can used in everyday speech.
In the first place, suppose we have a computer program that decides what to do by reasoning. Then its output is determined by the decisions it makes in the reasoning process. It does not know (has not computed) in advance what it will do, and, therefore, it is appropriate that it considers that it can do anything that can be achieved by some sequence of its outputs. Common-sense reasoning seems to operate in the same way.
The above rather simple notion of can requires some elaboration, both to represent adequately the commonsense notion and for practical purposes in the reasoning program.
First, suppose that the system of automata admits external
inputs. There are two ways of defining can in this case. One way
is to assert 
if p can achieve regardless of what
signals appear on the external inputs. Thus, we require
the existence of a sequence of outputs of p that achieves the goal
regardless of the sequence of external inputs to
the system. Note that, in this definition of can, we are
not requiring that p have any way of knowing what the external
inputs were. An alternative definition requires the outputs to
depend on the inputs of p. This is equivalent to saying that p
can achieve a goal, provided the goal would be achieved for arbitrary
inputs by some automaton put in place of p. With either of these
definitions can becomes a function of the place of the subautomaton
in the system rather than of the subautomaton itself. Both of these
treatments are likely to be useful, and so we shall call the
first concept cana and the second canb.
