The Original Missionaries and Cannibals Problem

The missionaries and cannibals problem (abbreviated MCP):

Three missionaries and three cannibals come to a river and find a boat that holds two. If the cannibals ever outnumber the missionaries on either bank, the missionaries will be eaten.

How shall they cross?

We call this original version of the problem MCP0.

Saul Amarel proposed [Ama71]: Let a state $(mcb)$ be given by the numbers of missionaries, cannibals and boats on the initial bank of the river. The initial situation is represented by $331$ and the goal situation by $000$.

Most AI texts that mention the problem accept this formulation and give us the solution:

$$331 \rightarrow 310 \rightarrow 321 \rightarrow 300 \right... ...ightarrow 031 \rightarrow 010 \rightarrow 021 \rightarrow 000.$$

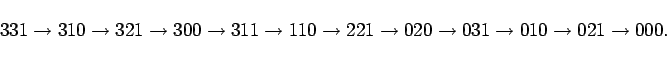
The state space of the Amarel repreentation has 32 elements some of which are forbidden and two of which are unreachable. It is an elementary student exercise to write a program to search the space and get the above sequence of states, and people are always solving it without a computer or without even a pencil. Saul Amarel [Ama71] points out that this representation has fewer states than a representation with named missionaries and cannibals.

What more does this problem offer AI?

If one indeed begins with the Amarel representation, the problem is indeed trivial. However, suppose we want a program that begins, as people do, with a natural language presentation of the problem. It is still trivial if the program need only solve the missionaries and cannibals problem. The programmer can then cheat as much as he likes by making his program exactly suited to the MCP. The extreme of cheating is to make a program that merely prints

$$331 \rightarrow 310 \rightarrow 321 \rightarrow 300 \right... ...ightarrow 031 \rightarrow 010 \rightarrow 021 \rightarrow 000.$$

Readers will rightly complain that this cheats, but it isn't clear what does and doesn't count as cheating when a method for solving a single problem is asked for.

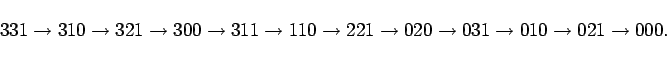
The way to disallow cheating is to demand a program that can solve any problem in a suitable set of problems. To illustrate this we consider a large set of elaborations of MCP. It won't be trivial to make a program that can solve all of them unless the human sets up each of them as a state space search analogous to the original MCP. We demand that the program use background common sense knowledge like that about rivers and boats that is used by a human solver.

We skip the part about going from an English statement of the problem to a logical statement for two reasons. First, we don't have anything new to say about parsing English or about the semantics of English. Second, we don't yet have the logical target language that the parsing program should aim at. Progress toward establishing this language is the goal of the paper.

The problem is then to make a program that will solve any of the problems using logically expressed background knowledge. The background knowledge should be described in a general way, not specifically oriented to MCP and related problems.

This much was already proposed in [McC59]. What is new in the present paper is spelling out the idea of elaboration tolerance that was distantly implicit in the 1959 paper. We require a formulation of MCP that readily tolerates elaborations of the problem and allows them to be described by sentences added to the statement of the problem rather than by surgery on the problem. We can call these additive elaborations. English language formulations allow this, but the Amarel-type formulations do not. AI requires a logical language that allows elaboration tolerant formulations.

We begin a few examples of English language elaboration tolerance. After discussing situation calculus formalisms, there will be a lot more.

• The boat is a rowboat. (Or the boat is a motorboat). This elaboration by itself should not affect the reasoning. By default, a tool is usable. Later elaborations make use of specific properties of rowboats.

• There are four missionaries and four cannibals. The problem is now unsolvable.

• There is an oar on each bank. One person can cross in the boat with just one oar, but two oars are needed if the boat is to carry two people.

• One of the missionaries is Jesus Christ. Four can cross. Here we are using cultural literacy. However, a human will not have had to have read Mark 6:48-49 to have heard of Jesus walking on water.

• Three missionaries with a lone cannibal can convert him into a missionary.

A later section discusses the formal problems of these and other elaborations.