Remarks.

 

1. Suppose a customer of type i has a probability 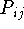of including item j in a basket. We can infer an approximate number of types by looking at the approximate rank of the matrix .
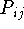2. Classifying customers into discrete types may not give as good results as a more complex model that take into account the age of the customer as a continuous variable.
3. A linear relation between phenomena and observations is the simplest case, and such relations can probably discovered by methods akin to factor analysis.
4. We could infer that there were two subpopulations if we didn't already know about sex.
5. We might infer from data from our stores in India, that there was a substantial part of the population that didn't purchase meat products. We can tell this from a situation in which everyone buys meat but less, because certain other purchase patterns are associated with not buying meat.
6. Tire mounting services are purchased in connection with the purchase of tires. The phenomenon is that tires are useless unless mounted. Does knowing this fact give more than just the correlation?
7. Suppose a new item, e.g. a hula hoop, is increasing its sales rapidly, and 5 percent of the customers have bought it. Suppose, however, that the customers that buy it rarely buy another, and these customers are only those with young girls in the family, and those customers have almost all bought one. Under these hypotheses, which identifying customers might verify, it is reasonable to conclude that the fad for hula hoops has reached its peak, and that if a lot more are ordered, the store is likely to be stuck with them.
8. Suppose we have the baskets grouped by customer--either because the data was given or because we have inferred it as described above. Can we determine how far the customers live from the store? The information might be useful in anticipating how much business might be lost to a newly opened competitor. No immediate idea occurred to me when I thought of the question. However, it is rash to conclude that it can't be done. Someone cleverer than I, or who knows more about customers of supermarkets, might figure a way. One just shouldn't jump to negative conclusions.
9. Grouping by customer might permit observing that no-one who buys item 531 ever buys anything from that store again. Such a fact would not show up as a direct correlation in the data unless item 531 were bought in quantities that significantly affected sales of some other items.
10. If a customer buys a certain product but doesn't buy a necessary complementary product, we can infer that he buys the complementary product from someone else.

The only experimental work with phenomenal data mining is reported in [LT98].