Suppose a function f is defined recursively by
(1) 
{ 
}
where 
is an expression that in general contains f. Suppose
that 
is the set of n-tuples 
for which f is
defined. Now let g and h be two other functions with the same
domain as f and which are defined for all n-tuples in . Suppose further that g and h satisfy the equation which
defined f. We assert that
for all in . This is so, simply because
equation (1) uniquely determines the value that any function
satisfying it has for arguments in which in turn follows
from the fact that (1) can be used to compute 
for
in .
We shall call this method of proving two functions equivalent by the name of recursion induction.
We shall develop some of the properties of the elementary functions of integers in order to illustrate proof by recursion induction. We recall the definitions
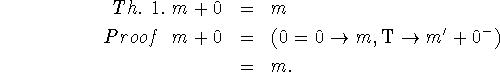
Only the definition of addition and the properties of conditional expressions
were used in this proof.
Proof Define 
. It is easily seen that f(m,n) converges for all m and
n and hence is completely defined by the above equation and is
computable from it. Now
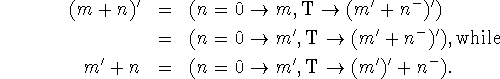
It is easily seen that the functions g and h defined by the equations g(m,n) =(m + n)' and h(m,n) = m' + n both satisfy the equation f. For example, it is
clear that 
and 
Therefore, by the principle of recursion induction h and g are equivalent functions on the domain
of where f is defined, but this is the set of all pairs of integers.
The fact that the above defined f(m,n) converges for all m and n is a case of the more general fact that all functions defined by equations of the form
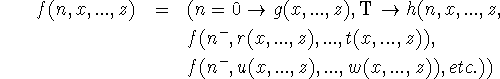
converge. We are not yet able to discuss formal proofs of convergence.
In presenting further proofs we shall be more terse.
Proof Let 
Again f converges for all m, n, p. We have
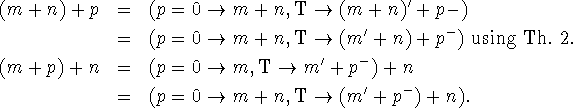
Each of these forms satisfies the equation for f(m,n,p).
Setting m = 0 in Theorem 3 gives
so that if we had 0 + m = m we would have commutativity of addition.
In fact, we cannot prove 0 + m = m without making some assumptions that take into account that we are dealing with the integers. For suppose our space consisted of the vertices of the binary tree in figure 2, where
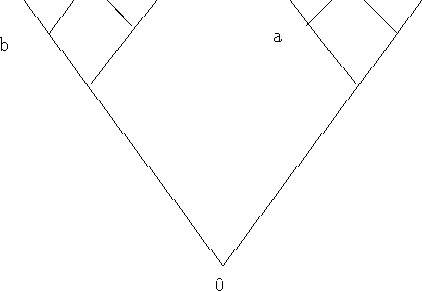
Fig. 2
m' is the vertex just above and to the left, and 
is the vertex
just below, and 0 is the bottom of the tree. m + n can be defined as
above and of course satisfies Theorems 1, 2, and 3 but does not
satisfy 0+m = m. For example, in the diagram 0 + a = b although a
+ 0 = a.
We shall make the following assumptions:
1. 
2. 
3. 
which embody all of Peano's axioms except the induction axiom.
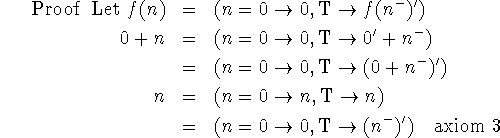
Proof By 3 and 4 as remarked above.
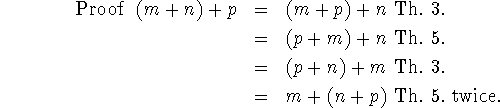
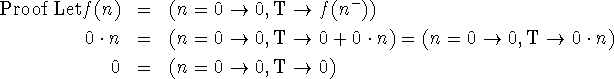
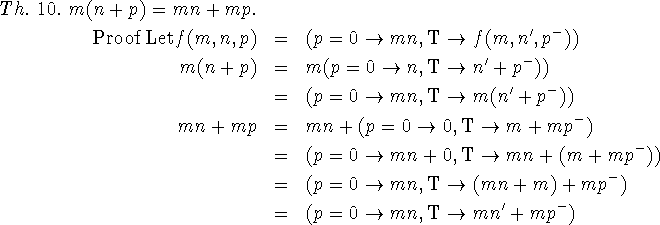
Now we shall give some examples of the application of recursion induction to proving theorems about functions of symbolic expressions. The rest of these proofs depend on an acquaintance with the Lisp formalism.
We start with the basic identities.
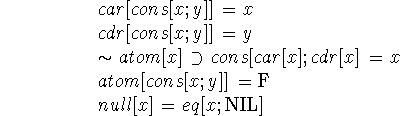
Let us define the concatenation 
of two lists x and y by the formula
Our first objective is to show that concatenation is associative.
Th. 11. 
Proof
We shall show that 
and 
satisfy the functional equation
First we establish an auxiliary result:
Now we write
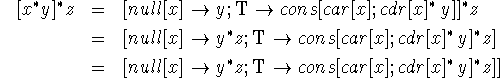
and
From these results it is obvious that both and 
satisfy the functional equation.
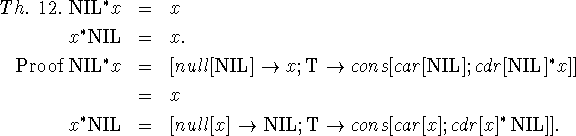
Let 
NIL satisfies this equation. We can also write for any list x
which also satisfies the equation.
Next we consider the function reverse[x] defined by
It is not difficult to prove by recursion induction that
and
Many other elementary results in the elementary theory of numbers and in the elementary theory of symbolic expressions are provable in the same straightforward way as the above. In number theory one gets as far as the theorem that if a prime p divides ab, then it divides either a or b. However, to formulate the unique factorization theorem requires a notation for dealing with sets of integers. Wilson's theorem, a moderately deep result, can be expressed in this formalism but apparently cannot be proved by recursion induction.
One of the most immediate problems in extending this theory is to develop better techniques for proving that a recursively defined function converges. We hope to find some based on ambiguous functions. However, Godel's theorem disallows any hope that a complete set of such rules can be formed.
The relevance to a theory of computation of this excursion into number
theory is that the theory illustrates in a simple form mathematical
problems involved in developing rules for proving the equivalence of
algorithms. Recursion induction, which was discovered by considering
number theoretic problems, turns out to be applicable without change
to functions of symbolic expressions.