The Blocks World as an Approximate Theory

 

The usual AI situation calculus blocks world has a propositional fluent asserting that block x is on block y. We can assert about some situation s and have the action that moves block x on top of block y.

Suppose this formalism is being used by a robot acting in the real world. The concepts denoted by , etc. are then approximate concepts, and the theory is an approximate theory. Our goal is to relate this approximate theory to the real world. Similar considerations would apply if we were relating it to a more comprehensive but still approximate theory.

We use formalized contexts as in [McC93b] and [MB97]. and let 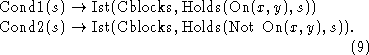be a blocks world context with a language allowing On(x,y), etc.

is approximate in at least the following respects.

• In the original intended interpretation of the situation calculus, a situation s is a snapshot of the world at a given time. According to the theory of relativity, distant simultaneity is ill-defined. This is the least of our worries.
• Whether block x is on block y may be ambiguous in the real world. Block x may be partly on and partly off. We can handle the relation by sentences

   

  and are respectively conditions in the outer context on the situation s that x shall be on y and x shall not be on y in the context 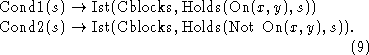. These need not be the negations of each other, so it can happen that it isn't justified to say either that x is on y or that it isn't. and need not be mutually exclusive. In that case the theory associated with 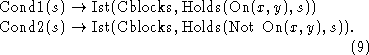would be inconsistent. However, unless there are strong lifting rules the inconsistency within 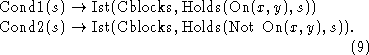cannot infect the rest of the reasoning.

Notice that the theory in the context 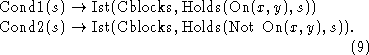approximates a theory in which blocks can be in different orientations on each other or in the air or on the table in quite different sense than numerical approximation.