

Next: What kinds of approximate
Up: APPROXIMATE OBJECTS AND APPROXIMATE
Previous: APPROXIMATE OBJECTS AND APPROXIMATE
We propose to extend the ontology of logical AI to include
approximate objects, approximate predicates and approximate
theories. Besides the ontology we discuss relations among different
approximations to the same or similar phenomena.
The article will be as precise as we can make it. We apply
Aristotle's remark to the approximate theories themselves. The
article treats three topics.
- Approximate objects
- These are not fully defined, e.g. the
wishes of the United States. They may be approximations to more
fully defined objects or they may be intrinsically approximate
(partial). We give lots of examples, because we don't have precise
definitions.
- Approximate theories
- These often involve necessary conditions
and sufficient conditions but lack conditions that are both
necessary and sufficient.
- Relations among approximate entities
- It is often necessary to
relate approximate entities, e.g. objects or theories, to less
approximate entities, e.g. to relate a theory in which one block is
just on another to a theory in which a block may be in various
positions on another.
In principle, AI theories, e.g. the original proposals for situation
calculus, have allowed for rich entities which could not be
fully defined. However, almost all theories used in existing AI
research has not taken advantage of this generality.
Logical AI theories have resembled formal scientific theories
in treating well-defined objects in well-defined domains.
Human-level AI will require reasoning about approximate entities.
Approximate predicates can't have complete if-and-only-if
definitions and usually don't even have definite extensions. Some
approximate concepts can be refined by learning more and some by
defining more and some by both, but it isn't possible in general to
make them well-defined. Approximate concepts are essential
for representing common sense knowledge and doing common sense
reasoning. In this article, assertions involving approximate concepts are
represented in mathematical logic.
A sentence involving an approximate concept may have a definite
truth value even if the concept is ill-defined. It is definite that
Mount Everest was climbed in 1953 even though exactly what rock and
ice is included in that mountain is ill-defined. We discuss the
extent to which we can build solid intellectual structures on such
swampy conceptual foundations.
Quantitative approximation is one kind considered--but not the most
interesting or the kind that requires logical innovation. Fuzzy
logic involves a semi-quantitative approximation, although
there are extensions as mentioned in [Zad99].
For AI purposes, the key problem is relating different approximate
theories of the same domain. For this we use mathematical logic
fortified with contexts as objects. Further innovations in logic may
be required to treat approximate concepts as flexibly in logic as
people do in thought and language.
Looked at in sufficient detail, all concepts are approximate, but
some are precise enough for a given purpose. McCarthy's weight
measured by a scales is precise enough for medical advice, and can
be regarded as exact in a theory of medical advice. On the other
hand, McCarthy's purposes are approximate enough so that almost any
discussion of them is likely to bump against its imprecision and
ambiguity.
Many concepts used in common sense reasoning are imprecise.
Here are some questions and issues that arise.
- What rocks and ice constitute Mount Everest?
- When can it be said that one block is on another block, so that
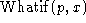 may be asserted?
may be asserted?
Let there be an axiomatic
theory in situation calculus in which it can be shown that a
sequence of actions will have a certain result. Now suppose that a
physical robot is to observe that one block is or is not on another
and determine the actions to achieve a goal using situation
calculus. It is important that the meanings of
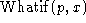 used in solving the problem theoretically and that used by the robot
correspond well enough so that carrying out a plan physically has the
desired effect. How well must they correspond?
used in solving the problem theoretically and that used by the robot
correspond well enough so that carrying out a plan physically has the
desired effect. How well must they correspond?
- What are the logical relations between different logical
specifications of an approximate object?
- What are the relations between different approximate logical
theories of a domain?
We claim
- The common sense informatic situation often involves
concepts which cannot be made precise. This is a question of the
information available and not about computation power. It is not a
specifically human limitation and will apply to computers of any
possible power. This is not a claim about physics; it may be that a
discoverable set of physical laws will account for all phenomena.
It is rather a question of the information actually available about
particular situations by people or robots with limited opportunities
to observe and compute.
- Much pedantry in science and in philosophy results from
demanding if-and-only-if definitions when this is
inappropriate.
- None of the above objects and predicates admits a completely precise
if-and-only-if definition.
- Formalized scientific theories, e.g. celestial mechanics and the
blocks world often have precise concepts. They are necessary tools
for understanding and computation. However, they are imbedded in
common sense knowledge about how to apply them in world of imprecise
concepts. Moreover, the concepts are precise only within the
theory. Most AI theories have also had this character.
- Almost all concepts are approximate in the full common sense
informatic situation. However, many are precise, i.e. have
if-and-only-if definitions in particular contexts.
- The human reasoning processes involving common sense knowledge
correspond only partly to the mathematical and logical reasoning
processes that humans have used so successfully within scientific
and mathematical theories.
- Nevertheless, mathematical logic is an appropriate tool
for representing this knowledge and carrying out this reasoning in
intelligent machines. The use of logic will certainly require
adaptations, and the logic itself may require modifications.
- Key tools for common sense reasoning by machines will be
approximate concepts and approximate theories. These
are in addition to formalized non-monotonic reasoning and
formal theories of context.
- The most important notion of approximation for common sense
reasoning is not the familiar numerical approximation but a new kind
of logical approximation appropriate for common sense reasoning.
These mostly differ from the approximations of fuzzy logic.
In the subsequent sections of this article, tools will be proposed for
reasoning with approximate concepts.
The article treats successively approximate objects,
approximate theories, and formalisms for describing how one
object or theory approximates another.


Next: What kinds of approximate
Up: APPROXIMATE OBJECTS AND APPROXIMATE
Previous: APPROXIMATE OBJECTS AND APPROXIMATE
John McCarthy
Wed Feb 2 15:59:04 PST 2000
![]() used in solving the problem theoretically and that used by the robot
correspond well enough so that carrying out a plan physically has the
desired effect. How well must they correspond?
used in solving the problem theoretically and that used by the robot
correspond well enough so that carrying out a plan physically has the
desired effect. How well must they correspond?