Our robot will also have to reason about its own knowledge and that of other robots and people.
This section contrasts the approaches to knowledge and belief characteristic of philosophy, philosophical logic and artificial intelligence. Knowledge and belief have long been studied in epistemology, philosophy of mind and in philosophical logic. Since about 1960, knowledge and belief have also been studied in AI. (Halpern 1986) and (Vardi 1988) contain recent work, mostly oriented to computer science including AI.
It seems to me that philosophers have generally treated knowledge and belief as complete natural kinds. According to this view there is a fact to be discovered about what beliefs are. Moreover, once it is decided what the objects of belief are (e.g. sentences or propositions), the definitions of belief ought to determine for each such object p whether the person believes it or not. This last is the completeness mentioned above. Of course, only human and sometimes animal beliefs have mainly been considered. Philosophers have differed about whether machines can ever be said to have beliefs, but even those who admit the possibility of machine belief consider that what beliefs are is to be determined by examining human belief.
The formalization of knowledge and belief has been studied as part of philosophical logic, certainly since Hintikka's book (1964), but much of the earlier work in modal logic can be seen as applicable. Different logics and axioms systems sometimes correspond to the distinctions that less formal philosophers make, but sometimes the mathematics dictates different distinctions.
AI takes a different course because of its different objectives, but I'm inclined to recommend this course to philosophers also, partly because we want their help but also because I think it has philosophical advantages.
The first question AI asks is: Why study knowledge and belief at all? Does a computer program solving problems and achieving goals in the common-sense world require beliefs, and must it use sentences about beliefs? The answer to both questions is approximately yes. At least there have to be data structures whose usage corresponds closely to human usage in some cases. For example, a robot that could use the American air transportation system has to know that travel agents know airline schedules, that there is a book (and now a computer accessible database) called the OAG that contains this information. If it is to be able to plan a trip with intermediate stops it has to have the general information that the departure gate from an intermediate stop is not to be discovered when the trip is first planned but will be available on arrival at the intermediate stop. If the robot has to keep secrets, it has to know about how information can be obtained by inference from other information, i.e. it has to have some kind of information model of the people from whom it is to keep the secrets.
However, none of this tells us that the notions of knowledge and belief to be built into our computer programs must correspond to the goals philosophers have been trying to achieve. For example, the difficulties involved in building a system that knows what travel agents know about airline schedules are not substantially connected with questions about how the travel agents can be absolutely certain. Its notion of knowledge doesn't have to be complete; i.e. it doesn't have to determine in all cases whether a person is to be regarded as knowing a given proposition. For many tasks it doesn't have to have opinions about when true belief doesn't constitute knowledge. The designers of AI systems can try to evade philosophical puzzles rather than solve them.
Maybe some people would suppose that if the question of certainty is avoided, the problems formalizing knowledge and belief become straightforward. That has not been our experience.
As soon as we try to formalize the simplest puzzles involving knowledge, we encounter difficulties that philosophers have rarely if ever attacked.
Consider the following puzzle of Mr. S and Mr. P.
Two numbers m and n are chosen such that ![]() .
Mr. S is told their sum and Mr. P is told their product. The following
dialogue ensues:
.
Mr. S is told their sum and Mr. P is told their product. The following
dialogue ensues:
Mr. P: I don't know the numbers.
Mr. S: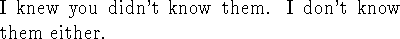
Mr. P: Now I know the numbers.
Mr. S: Now I know them too.
In view of the above dialogue, what are the numbers?
Formalizing the puzzle is discussed in (McCarthy 1989). For the present we mention only the following aspects.
1. We need to formalize knowing what, i.e. knowing what the numbers are, and not just knowing that.
2. We need to be able to express and prove non-knowledge as well as knowledge. Specifically we need to be able to express the fact that as far as Mr. P knows, the numbers might be any pair of factors of the known product.
3. We need to express the joint knowledge of Mr. S and Mr. P of the conditions of the problem.
4. We need to express the change of knowledge with time, e.g. how Mr. P's knowledge changes when he hears Mr. S say that he knew that Mr. P didn't know the numbers and doesn't know them himself. This includes inferring what Mr. S and Mr. P still won't know.
The first order language used to express the facts of this problem involves an accessibility relation A(w1,w2,p,t), modeled on Kripke's semantics for modal logic. However, the accessibility relation here is in the language itself rather than in a metalanguage. Here w1 and w2 are possible worlds, p is a person and t is an integer time. The use of possible worlds makes it convenient to express non-knowledge. Assertions of non-knowledge are expressed as the existence of accessible worlds satisfying appropriate conditions.
The problem was successfully expressed in the language in the sense that an arithmetic condition determining the values of the two numbers can be deduced from the statement. However, this is not good enough for AI. Namely, we would like to include facts about knowledge in a general purpose common-sense database. Instead of an ad hoc formalization of Mr. S and Mr. P, the problem should be solvable from the same general facts about knowledge that might be used to reason about the knowledge possessed by travel agents supplemented only by the facts about the dialogue. Moreover, the language of the general purpose database should accommodate all the modalities that might be wanted and not just knowledge. This suggests using ordinary logic, e.g. first order logic, rather than modal logic, so that the modalities can be ordinary functions or predicates rather than modal operators.
Suppose we are successful in developing a ``knowledge formalism'' for our common-sense database that enables the program controlling a robot to solve puzzles and plan trips and do the other tasks that arise in the common-sense environment requiring reasoning about knowledge. It will surely be asked whether it is really knowledge that has been formalized. I doubt that the question has an answer. This is perhaps the question of whether knowledge is a natural kind.
I suppose some philosophers would say that such problems are not of philosophical interest. It would be unfortunate, however, if philosophers were to abandon such a substantial part of epistemology to computer science. This is because the analytic skills that philosophers have acquired are relevant to the problems.